Pytorch框架RNN快速入门与实战
Pytorch框架RNN快速入门与实战
参考:https://blog.csdn.net/weixin_45727931/article/details/114369073
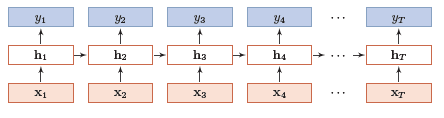
先简单聊聊RNN的结构。最简单的一层RNN网络结构如下图所示:
其中,每个箭头都表示一个权值,输入为向量X,输出向量为Y,隐含层向量为H。一层指的是有一层隐含层。也可以根据具体需求设计多层,一般层数取2-10。时间步共享参数。
RNN模块
Pytorch中RNN模块函数为torch.nn.RNN(input_size,hidden_size,num_layers,batch_first),每个参数的含义如下:
input_size:输入数据的编码维度,比如前面举例的房价预测,房价都是用一维的数直接表示的,所以此时input_size为1;如果输入的是字符编码,比如一个字符用3维编码表示,那么此时input_size为3;hidden_size:隐含层的维数,这个维数要么参考别人的结构设置,要么自行设置,比如可以设置成20;num_layers:隐含层的层数,也就是上面几幅图有几个h层,上面都是只有1层,所以num_layers为1。batch_first:当batch_first设置为True时,输入的参数顺序变为:x:[batch, seq_len, input_size],h0:[batch, num_layers, hidden_size]。当batch_first设置为 False 时,x:[seq_len, batch, input_size],h0:[num_layers, batch, hidden_size]
输入的表示
输入的表示形式,输入如下图所示,输入主要有向量 x 、初始的 $h_0$ , 其中x:[seq_len, batch, input_size],h0:[num_layers, batch, hidden_size],下面分别介绍每个参数的意义。
seq_len:输入的长度,即有多少个 $x_i$ ,上述房价预测中,如果输入的是12个月的房价,那么seq_len就为12,即时间步;batch:在训练神经网络时,可以多批次数据同时训练,还是以房价预测为例,现在同时拿去年,今年共两年的数据训练网络,也就是将两年的数据batch在了一起。input_size:与torch.nn.RNN中一致;num_layers:与torch.nn.RNN中一致;hidden_size:与torch.nn.RNN中一致;
输出的表示
输出可以是Y向量,也可以是最后一个时刻隐含层的输出 $h_T$ 。
如果输出是Y向量,那么Y向量的结构为out:[seq_len, batch, hidden_size],每个参数的意义与上面一致。
翻译任务
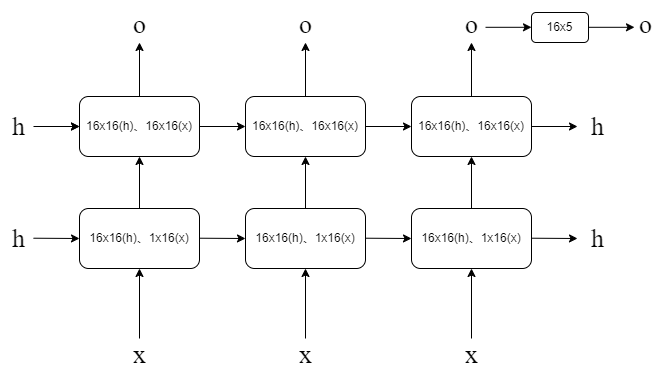
比如我现在想设计一个4层的RNN,用来做翻译,输入是一段中文,输出是一段英文。
- 每个中文字符用100维数据进行编码。
input_size = 100 - 每个隐含层的维度是20。
hidden_size = 20 - 有4个隐含层。
num_layers = 4 - 长度为10的句子做输入。
seq_len = 10 - 每次1个句子。
batch_size = 1
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch
import torch.nn as nn
input_size = 100 # 输入数据编码的维度
hidden_size = 20 # 隐含层维度
num_layers = 4 # 隐含层层数
seq_len = 10 # 句子长度
batch_size = 1
rnn = nn.RNN(input_size=input_size,hidden_size=hidden_size,num_layers=num_layers)
print("rnn:",rnn)
x = torch.randn(seq_len,batch_size,input_size) # 输入数据
h0 = torch.zeros(num_layers,batch_size,hidden_size) # 输入数据
out, h = rnn(x, h0) # 输出数据
print("out.shape:",out.shape)
print("h.shape:",h.shape)
输出:
1
2
3
rnn: RNN(100, 20, num_layers=4)
out.shape: torch.Size([10, 1, 20]) # [seq_len, batch, hidden_size]
h.shape: torch.Size([4, 1, 20]) # [num_layers, batch, hidden_size]
另外一个示例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import torch
from torch import nn
input_size = 1
hidden_size = 16
output_size = 5
num_layers = 2
seq_len = 3
batch_size = 4
class Net(nn.Module):
def __init__(self, input_size, hidden_size, num_layers):
super(Net, self).__init__()
self.rnn = nn.RNN(
input_size=input_size,
hidden_size=hidden_size,
num_layers=num_layers,
batch_first=True,
)
# 用正态分布初始化参数,防止梯度消失
for p in self.rnn.parameters():
nn.init.normal_(p, mean=0.0, std=0.001)
self.linear = nn.Linear(hidden_size, output_size)
def forward(self, x, hidden_prev):
# out: batch_size, seq_len, hidden_size, hidden_prev: num_layers, batch_size, hidden_size
out, hidden_prev = self.rnn(x, hidden_prev)
out = out[:, -1, :] # 取最后一个时间步的输出
out = self.linear(out)
return out, hidden_prev
net = Net(input_size, hidden_size, num_layers)
x = torch.randn(batch_size, seq_len, input_size)
h = torch.zeros(num_layers, batch_size, hidden_size)
print(net)
out, h = net(x, h)
print(out.shape) # batch_size, output_size
print(h.shape) # num_layers, batch_size, hidden_size
请思考一下为什么维度是这样的。
时序数据预测
假设现在有一系列3维飞机航迹数据,我们想预测接下来的航迹数据,那么可以考虑用RNN预测。首先设计网络:
- 每个航迹点都是3维的,所以
input_size = 3 - 隐含层
hidden_size = 16 - 有一个隐含层,所以
num_layers = 1
为了更好的利用数据,下面代码实现的是这样的功能:输入第[1,15]个数据,输出第[6,21]个数据,即往后平移5个单位的数据。
设置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import torch
import datetime
import numpy as np
import torch.nn as nn
import torch.optim as optim
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
seq_length = 300 # 训练时时间窗的长度
num_time_steps = 16 # 训练时时间窗的步长
input_size = 3 # 输入数据维度
hidden_size = 16 # 隐含层维度
output_size = 3 # 输出维度
num_layers = 1
lr=0.01
模型定义
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Net(nn.Module):
def __init__(self, input_size, hidden_size, num_layers):
super(Net, self).__init__()
self.rnn = nn.RNN(
input_size=input_size,
hidden_size=hidden_size,
num_layers=num_layers,
batch_first=True,
)
# 用正态分布初始化参数,防止梯度消失
for p in self.rnn.parameters():
nn.init.normal_(p, mean=0.0, std=0.001)
self.linear = nn.Linear(hidden_size, output_size)
def forward(self, x, hidden_prev):
out, hidden_prev = self.rnn(x, hidden_prev)
# [b, seq, h]
out = out.view(-1, hidden_size)
out = self.linear(out)#[seq,h] => [seq,3]
out = out.unsqueeze(dim=0) # => [1,seq,3]
return out, hidden_prev
初始化训练集
1
2
3
4
5
6
7
8
9
10
11
12
def getdata():
"""
给出一个seq_length*3的矩阵,包含x,y,z三个坐标
"""
x1 = np.linspace(1,10,seq_length).reshape(seq_length,1) # linspace函数通过指定开始值、终值和元素个数来创建一维数组
y1 = (np.zeros_like(x1)+2)+np.random.rand(seq_length,1)*0.1
z1 = (np.zeros_like(x1)+2)+np.random.rand(seq_length,1)*0.1
for i in range(seq_length):
# y1[i] = y1[i] + np.sin(i)
z1[i] = z1[i] + np.cos(0.05*i)
tr1 = np.concatenate((x1,y1,z1),axis=1) # 按列合并,得到seq_length*3的矩阵
return tr1
训练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
def tarin_RNN(data):
model = Net(input_size, hidden_size, num_layers)
print('model:\n',model)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr)
hidden_prev = torch.zeros(1, 1, hidden_size) #初始化h
l = []
# 训练3000次
for iter in range(3000):
# loss = 0
start = np.random.randint(10, size=1)[0] # 随机生成一个0-10之间的整数
end = start + num_time_steps
# 在data里面随机选择num_time_steps,即15个点作为输入
x = torch.tensor(data[start:end]).float().view(1, num_time_steps, output_size)
# 预测目标后移5个时间步
y = torch.tensor(data[start + 5:end + 5]).float().view(1, num_time_steps, output_size)
output, hidden_prev = model(x, hidden_prev)
hidden_prev = hidden_prev.detach() # 将h从计算图中分离出来
loss = criterion(output, y)
model.zero_grad()
loss.backward()
optimizer.step()
if iter % 100 == 0:
print("Iteration: {} loss {}".format(iter, loss.item()))
l.append(loss.item())
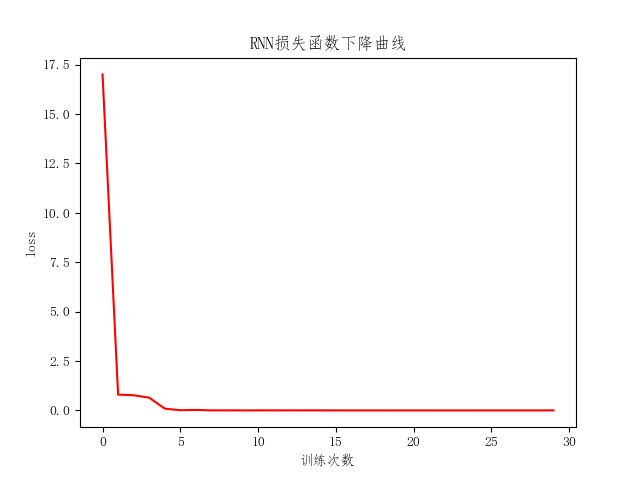
# 绘制损失函数
plt.plot(l,'r')
plt.xlabel('训练次数')
plt.ylabel('loss')
plt.title('RNN损失函数下降曲线')
return hidden_prev,model
预测
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def RNN_pre(model,data,hidden_prev):
data_test = data[19:29] # 选取最后10个点作为测试集
data_test = torch.tensor(np.expand_dims(data_test, axis=0),dtype=torch.float32)
predictions,h1 = model(data_test,hidden_prev)
predictions = predictions.detach().numpy().reshape(10,3)
print('predictions.shape:',predictions.shape)
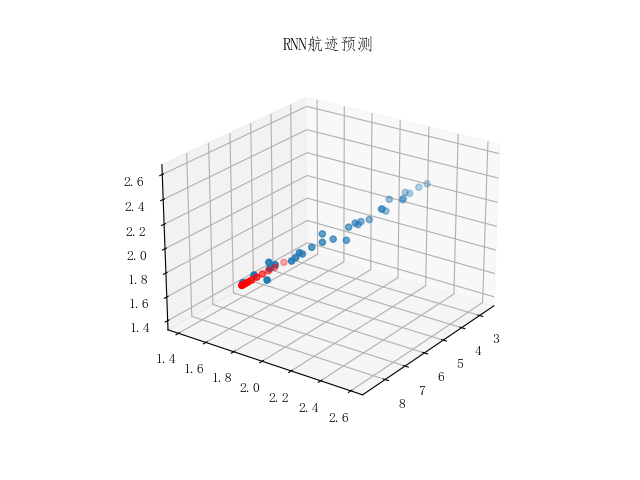
# 预测可视化
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(data[:, 0], data[:, 1], data[:, 2])
ax.scatter(predictions[:,0],predictions[:,1],predictions[:,2],c='r')
ax.set_ylim([1, 3])
ax.set_zlim([1, 3])
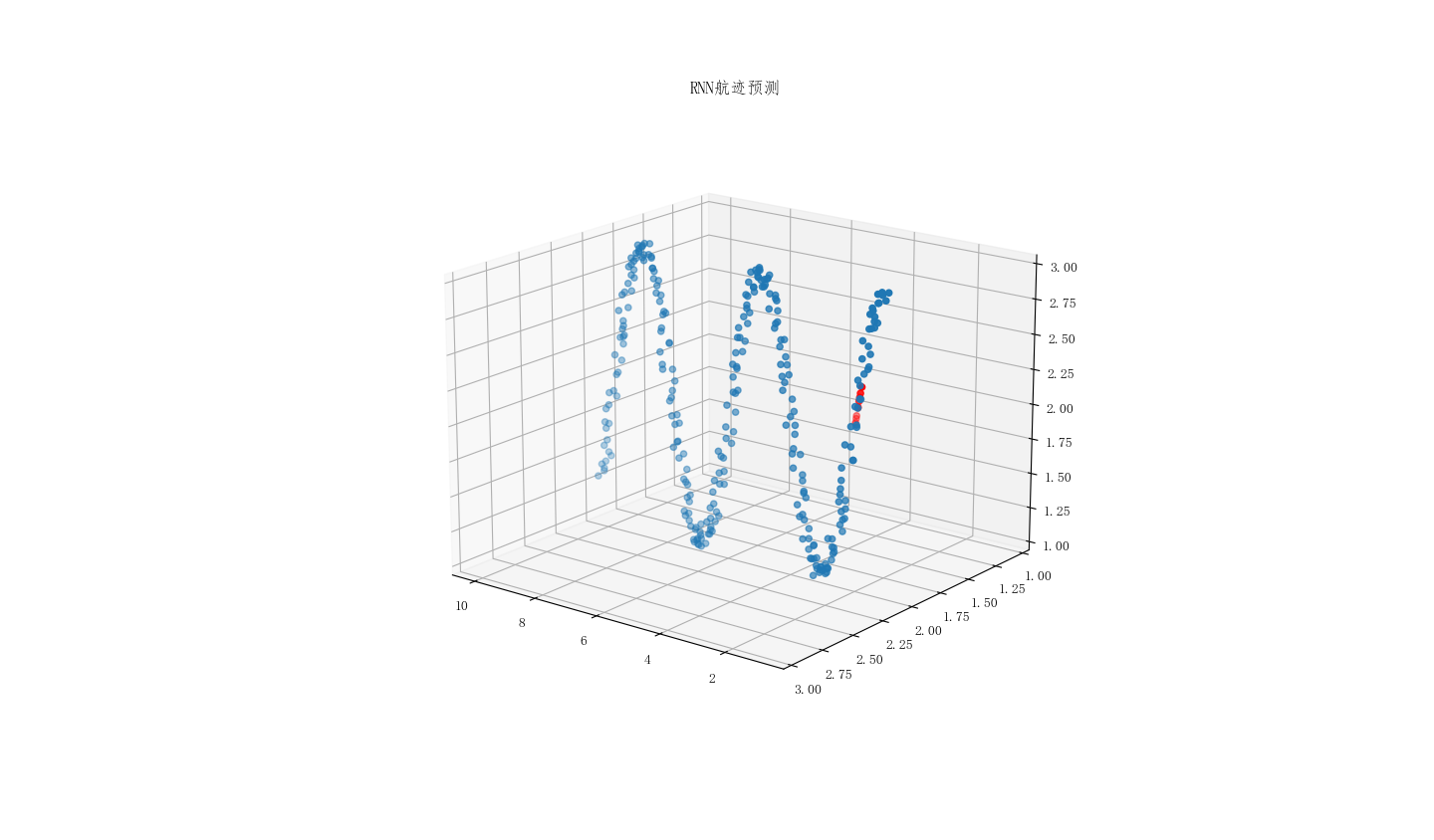
plt.title("RNN航迹预测")
plt.show()
main
1
2
3
4
5
6
7
8
9
10
11
def main():
data = getdata()
start = datetime.datetime.now()
hidden_pre, model = tarin_RNN(data)
end = datetime.datetime.now()
print('The training time: %s' % str(end - start))
plt.show()
RNN_pre(model, data, hidden_pre)
if __name__ == '__main__':
main()
结果
1
2
3
4
5
6
7
8
9
model:
Net(
(rnn): RNN(3, 16, batch_first=True)
(linear): Linear(in_features=16, out_features=3, bias=True)
)
Iteration: 0 loss 19.033266067504883
...
Iteration: 2900 loss 0.001077626715414226
The training time: 0:00:02.653348
本文由作者按照 CC BY 4.0 进行授权