Siamese Network & Triplet NetWork
Siamese Network(孪生网络)
简单来说,孪生网络就是共享参数的两个神经网络。
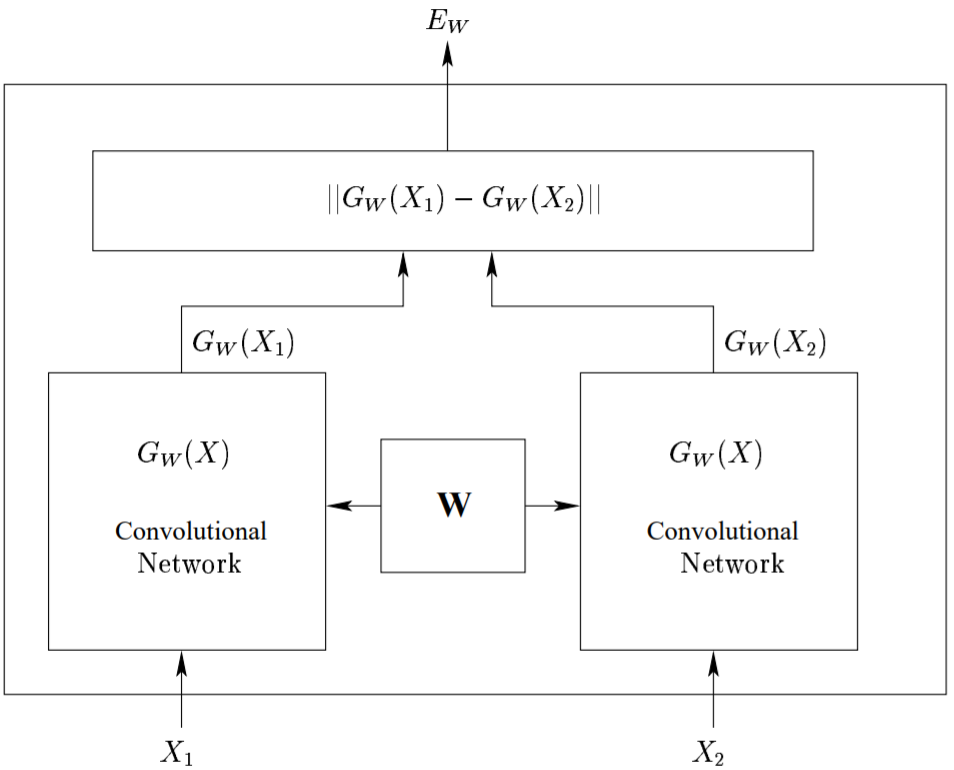
在孪生网络中,我们把一张图片 X1 作为输入,得到该图片的编码 $G_W(X_1)$。然后,我们在不对网络参数进行任何更新的情况下,输入另一张图片 W2,并得到改图片的编码 $G_W(X_2)$。由于相似的图片应该具有相似的特征(编码),利用这一点,我们就可以比较并判断两张图片的相似性
对比损失函数
传统的 Siamese Network 使用 Contrastive Loss(对比损失函数)
\[\mathcal{L} = (1-Y)\frac{1}{2}(D_W)^2+(Y)\frac{1}{2}\{max(0, m-D_W)\}^2\]其中$D_W$被定义为孪生网络两个输入之间的欧氏距离,即
\[D_W = \sqrt{\{G_W(X_1)-G_W(X_2)\}^2}\]- Y值为 0 或 1,如果 X1, X2 这对样本属于同一类,则 Y=0,反之 Y=1
- m是边际价值(margin value),即当 Y=1,如果 X1 与 X2 之间距离大于 m,则不做优化(省时省力);如果 X1 与 X2 之间的距离小于 m,则调整参数使其距离增大到 m
代码:
1
2
3
4
5
6
7
8
9
10
11
class ContrastiveLoss(torch.nn.Module):
"Contrastive loss function"
def __init__(self, m=2.0):
super(ContrastiveLoss, self).__init__()
self.m = m
def forward(self, output1, output2, label):
d_w = F.pairwise_distance(output1, output2)
contrastive_loss = torch.mean((1-label) * 0.5 * torch.pow(d_w, 2) +
(label) * 0.5 * torch.pow(torch.clamp(self.m - d_w, min=0.0), 2))
return contrastive_loss
孪生网络的用途
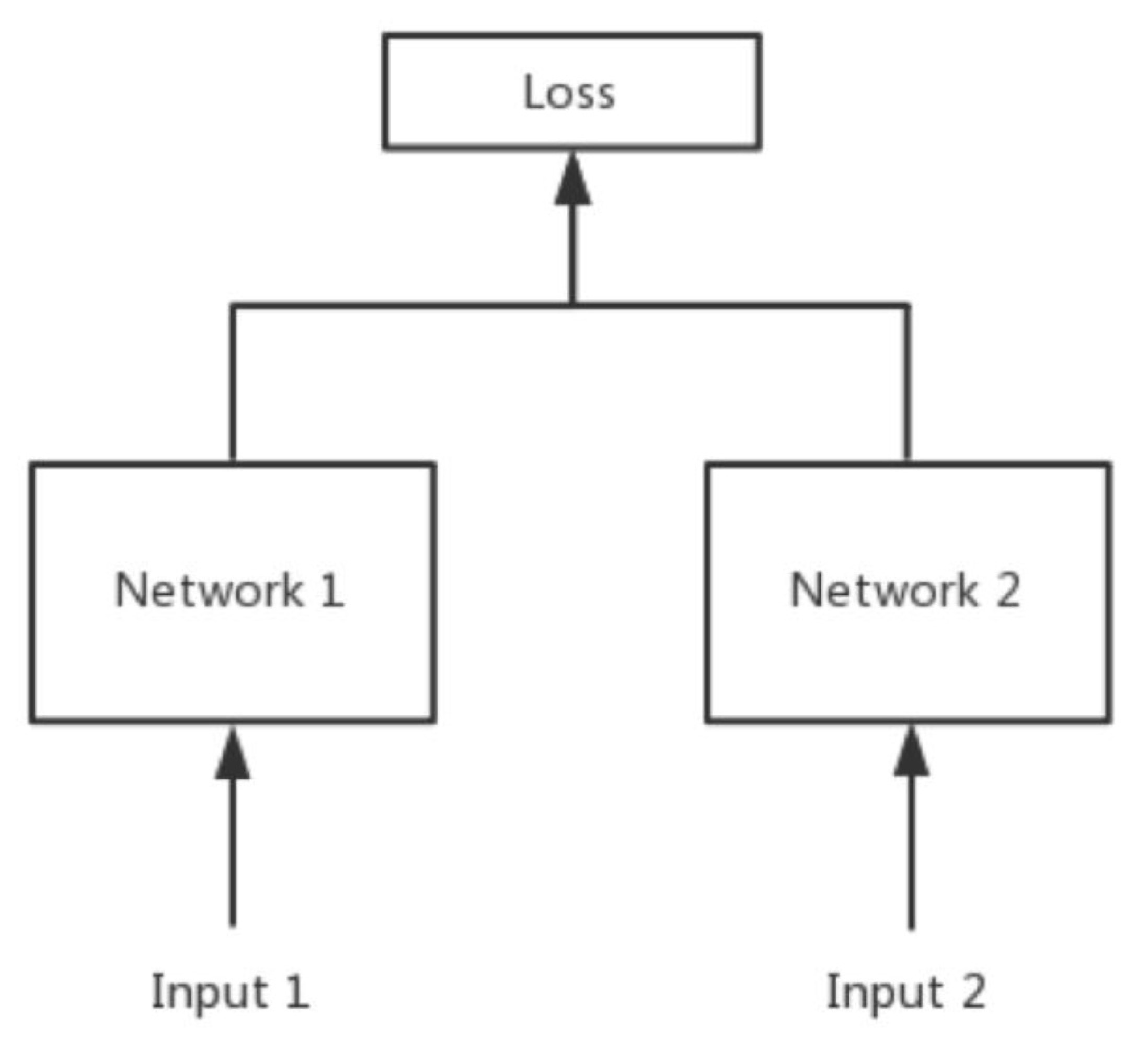
简单来说,孪生网络的直接用途就是衡量两个输入的差异程度(或者说相似程度)。将两个输入分别送入两个神经网络,得到其在新空间的 representation,然后通过 Loss Function 来计算它们的差异程度(或相似程度)
- 词汇语义相似度分析,QA 中 question 和 answer 的匹配
- 手写体识别也可以用 Siamese Network
- Kaggle 上 Quora 的 Question Pair 比赛,即判断两个提问是否为同一个问题
Pseudo-Siamese Network(伪孪生网络)
对于伪孪生网络来说,两边可以是不同的神经网络(如一个是 lstm,一个是 cnn),并且如果是相同的神经网络,是不共享参数的。
孪生网络和伪孪生网络分别适用的场景:
- 孪生网络适用于处理两个输入比较类似的情况
- 伪孪生网络适用于处理两个输入有一定差别的情况
例如,计算两个句子或者词汇的语义相似度,使用 Siamese Network 比较合适;验证标题与正文的描述是否一致(标题和正文长度差别很大),或者文字是否描述了一幅图片(一个是图片,一个是文字)就应该使用 Pseudo-Siamese Network
Triplet Network(三胞胎网络)
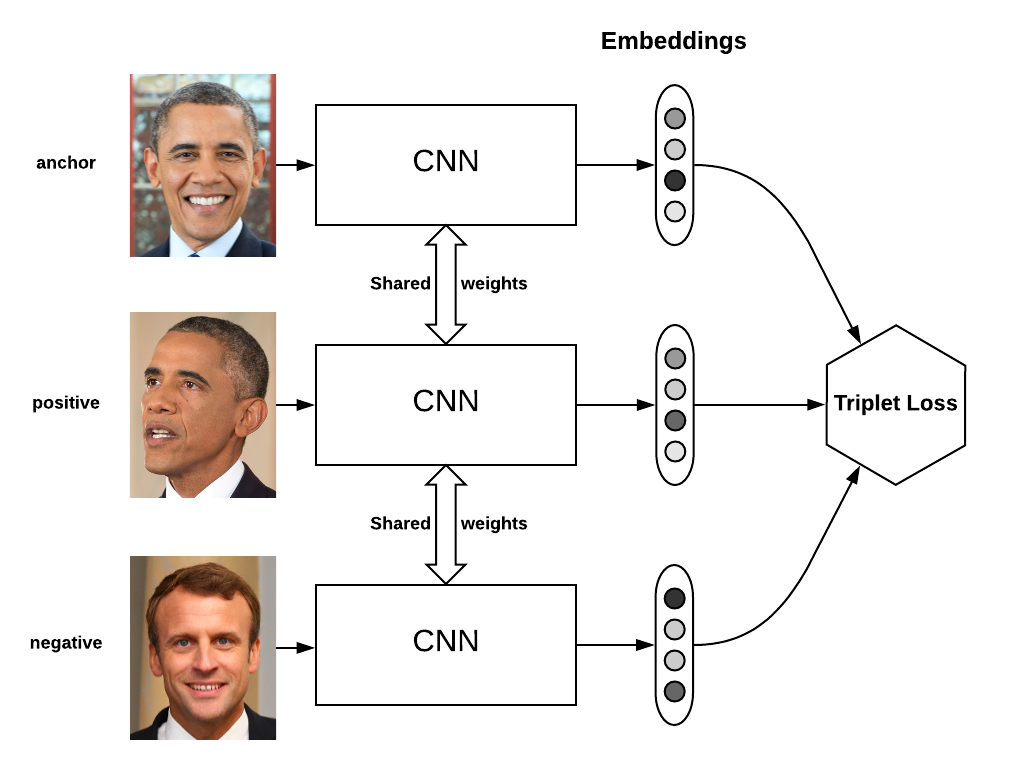
如果说 Siamese Network 是双胞胎,那 Triplet Network 就是三胞胎。它的输入是三个:一个正例 + 两个负例,或一个负例 + 两个正例。训练的目标仍然是让相同类别间的距离尽可能小,不同类别间的距离尽可能大。Triplet Network 在 CIFAR,MNIST 数据集上效果均超过了 Siamese Network
损失函数定义如下:
\[\mathcal{L}=max(d(a,p)-d(a,n)+margin, 0)\]- a 表示 anchor 图像
- p 表示 positive 图像
- n 表示 negative 图像
我们希望 a 与 p 的距离应该小于 a 与 n 的距离。margin 是个超参数,它表示 d(a,p) 与 d(a,n) 之间应该相差多少,例如,假设 margin=0.2,并且 d(a,p)=0.5,那么 d(a,n) 应该大于等于 0.7