读论文时间！
图卷积神经网络：GCN
参考：
简单实例：计算工资
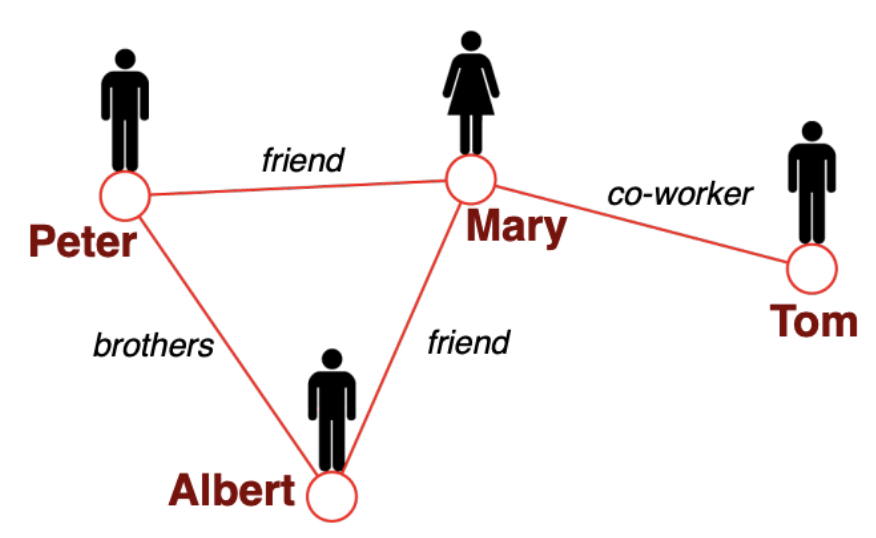
假设在一个人际关系图里面，人是节点，关系是边，要在这样一个图中预测某一个节点的工资。
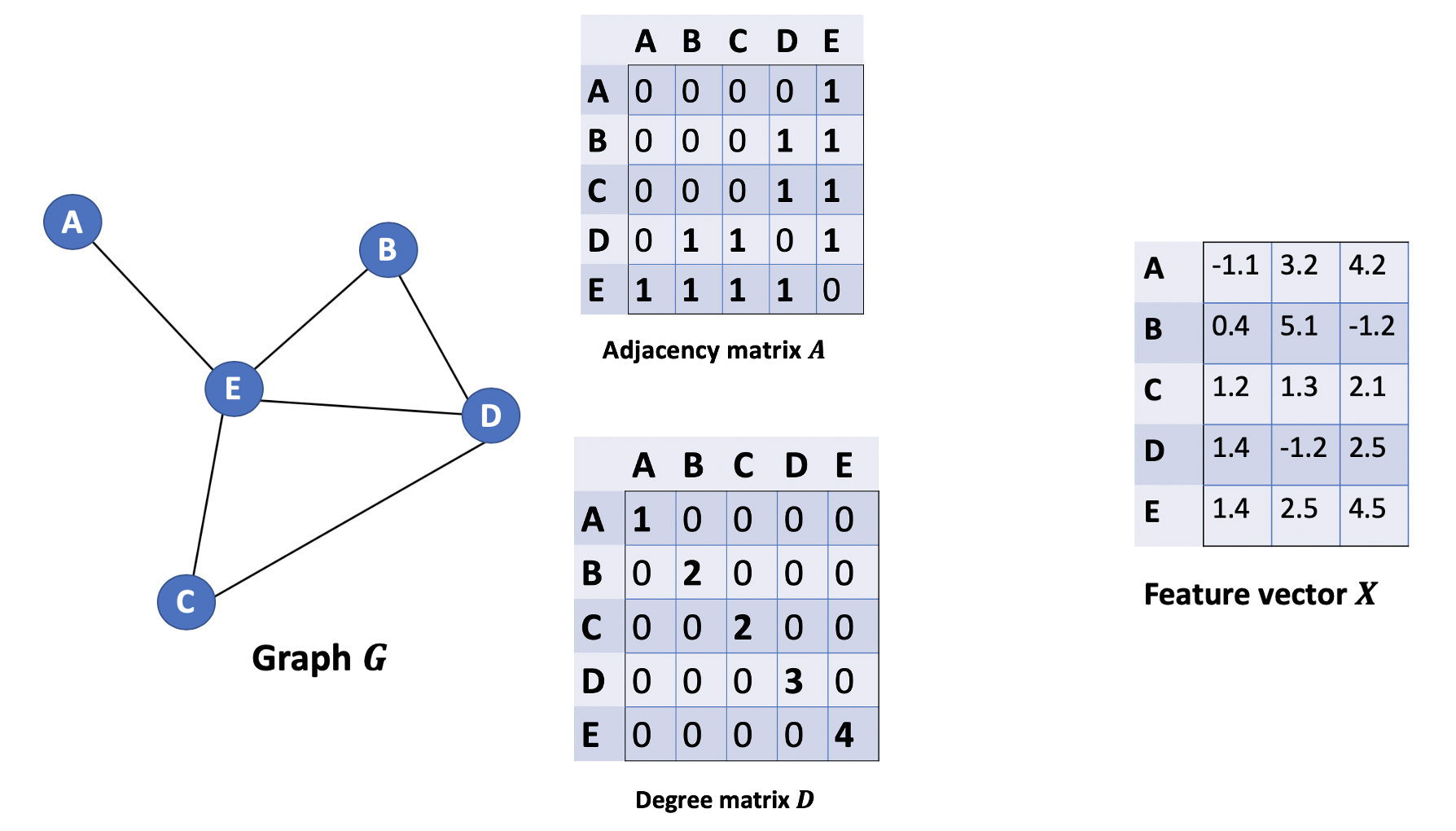
我们首先定义一下用到的矩阵。从图G中，我们有一个邻接矩阵A和一个度矩阵D。同时我们也有特征矩阵X。
第一个方案
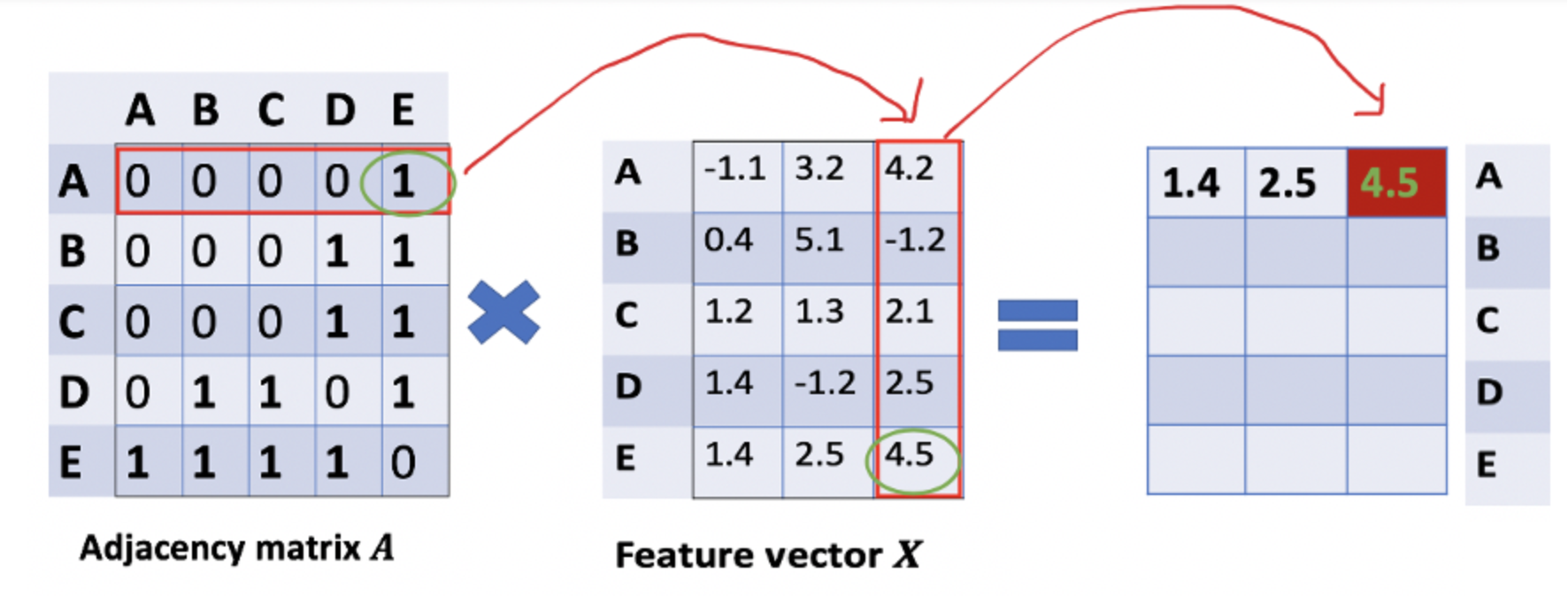
我们第一个方案是：一个节点（人）的工资是所有相邻节点工资的加和。解决方法是A和X的相乘。
\[AX\]看看邻接矩阵的第一行，我们看到节点A与节点E之间有连接，得到的矩阵第一行就是与A相连接的E节点的特征向量（如下图）。同理，得到的矩阵的第二行是D和E的特征向量之和，通过这个方法，我们可以得到所有邻居节点的向量之和。
这里还有一些需要改进的地方：
- 我们忽略了节点本身的特征。我的工资应该由我自己的能力来主要决定，不能忽略我本身的特征，只根据我周围的人来判断我的工资。
- 我们不需要使用sum()函数，而是需要取平均值，甚至更好的邻居节点特征向量的加权平均值。那我们为什么不使用sum()函数呢？原因是在使用sum()函数时，度大的节点很可能会生成的大的v向量，而度低的节点往往会得到小的聚集向量，这可能会在以后造成梯度爆炸或梯度消失（例如，使用sigmoid时）。此外，神经网络似乎对输入数据的规模很敏感。因此，我们需要对这些向量进行归一化，以摆脱可能出现的问题。
- 上面一点换句话说，我的工资应该更接近于我周围人工资的平均值，而不是这些工资的求和。
第二个方案
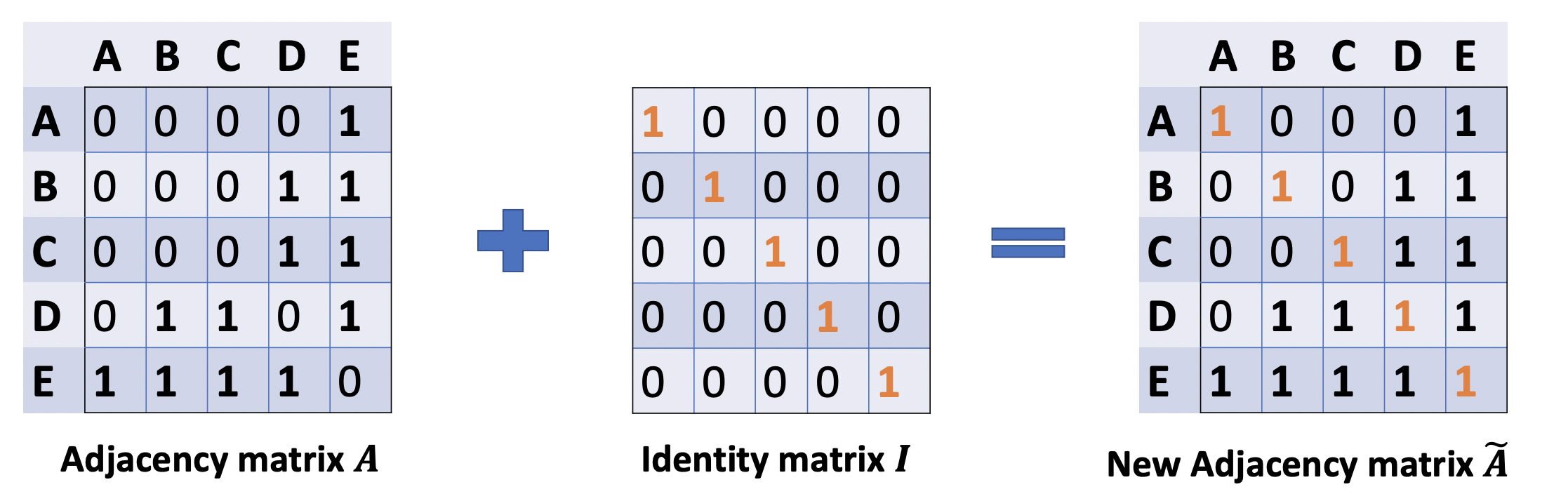
现在我们来尝试解决第一个问题，加入某个节点自己的特征。
我们可以通过在A中增加一个单位矩阵I来解决，得到一个新的邻接矩阵。
\[\tilde{A}=A+\lambda I\]取lambda=1（使得节点本身的特征和邻居一样重要），我们就有Ã=A+I，注意，我们可以把lambda当做一个可训练的参数，但现在只要把lambda赋值为1就可以了，即使在论文中，lambda也只是简单的赋值为1。
然后计算：
\[\tilde{A}X\]第三个方案
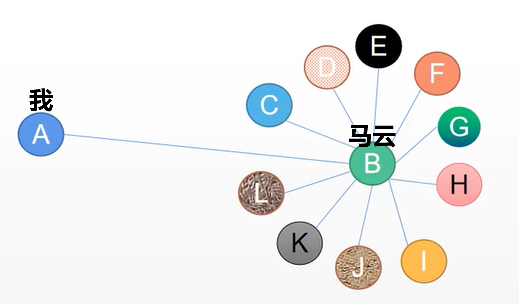
可以从一个生活化的角度来讲，例如我只有一个朋友是马云，那么我和他工资的平均值是不是就是我的工资？
肯定不对。问题在于：虽然我只有一个朋友是马云，但是马云认识几千几万个人，我只是其中的一个不重要的节点。
从数学角度上说，要根据节点度数对聚合向量矩阵ÃX进行缩放。直觉告诉我们这里用来缩放的对角矩阵是和度矩阵D̃有关的东西（为什么是D̃，而不是D？因为我们考虑的是新邻接矩阵Ã 的度矩阵D̃，而不再是A了）。
我们可以在每一个节点计算的时候加上这个：
\[\frac{1}{\sqrt{deg(v_i)} \cdot \sqrt{deg(v_j)}}\]意思是说：如果一个节点它的度很大，那么他对其他周围邻居的影响会变小。比如马云有十万个朋友，那么式子的分母很大，他对我的影响就非常小。
矩阵如何表示？如下（具体的证明略）：
\[\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}X\]让我们把式子整理一下：
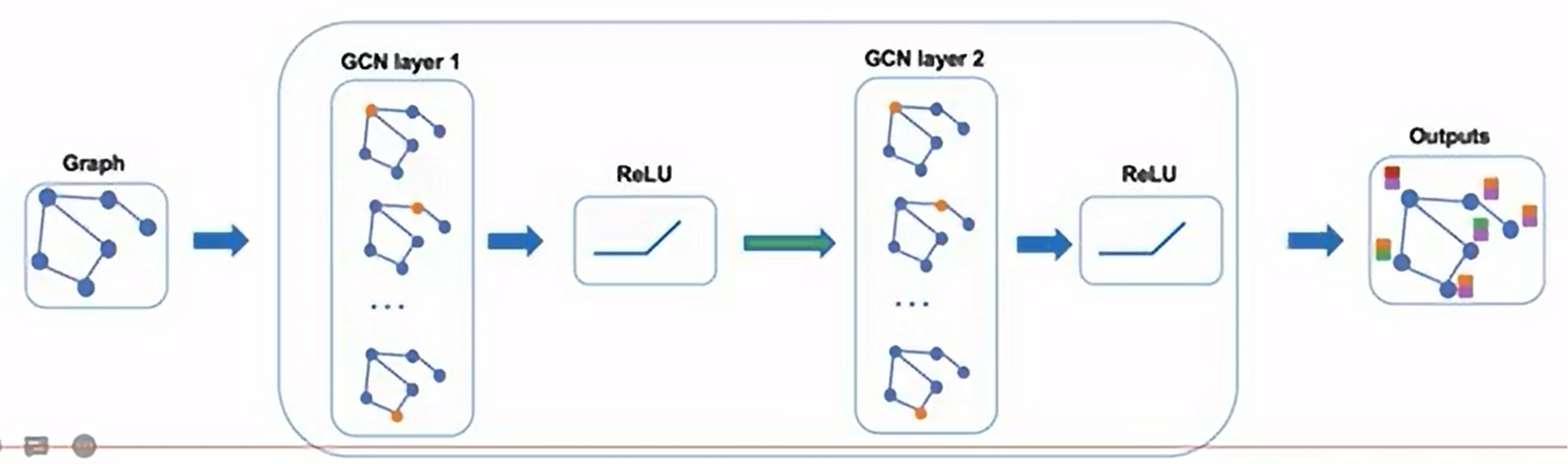
\[\tilde{A}=A+\lambda I\] \[H^{(l+1)}= \sigma( \tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2} H^{(l)}W^{(l)})\]之前我们举的例子都是在从同一层中做计算，当然如果我们熟悉图神经网络的基本原理的话，网络肯定是多层的，所以这边会出现 l 层和 l+1 层的参数。
- W：第l 层参数矩阵，可学习
- H：第 l 层的激活矩阵
模型层数
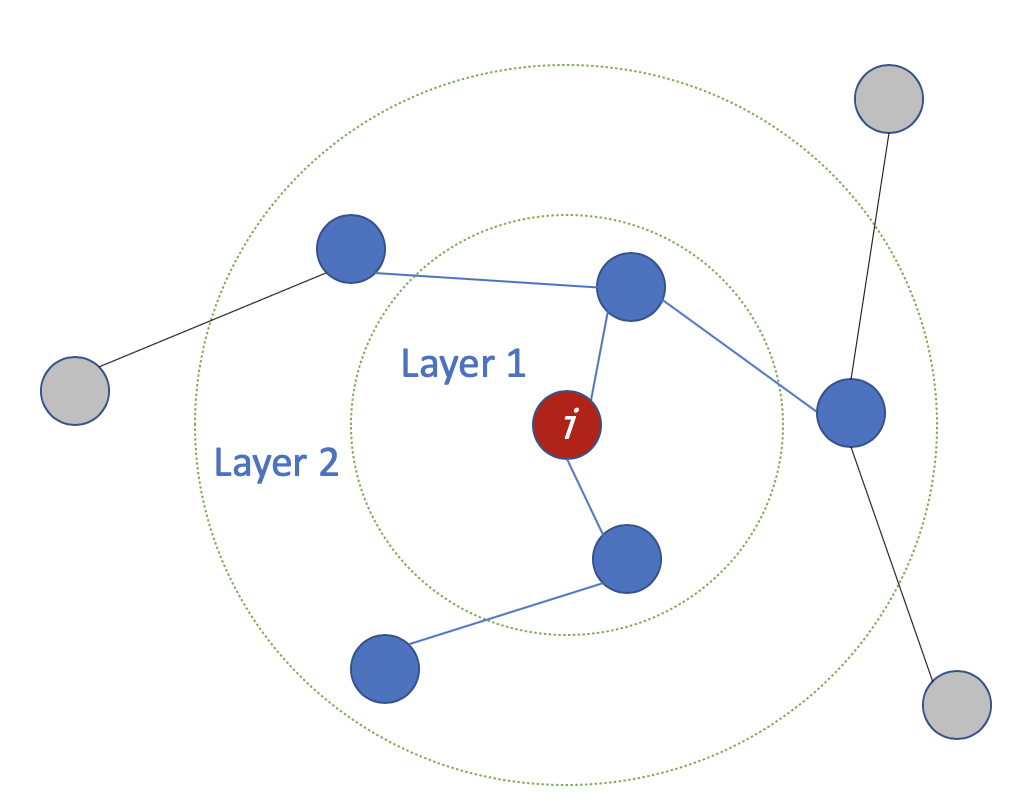
层数是指节点特征能够传输的最远距离。例如，在1层的GCN中，每个节点只能从其邻居那里获得信息。每个节点收集信息的过程是独立进行的，对所有节点来说都是在同一时间进行的。
当在第一层的基础上再叠加一层时，我们重复收集信息的过程，但这一次，邻居节点已经有了自己的邻居的信息（来自上一步）。这使得层数成为每个节点可以走的最大跳步。所以，这取决于我们认为一个节点应该从网络中获取多远的信息，我们可以为#layers设置一个合适的数字。
但同样，在图中，通常我们不希望走得太远。设置为6-7跳，我们就几乎可以得到整个图，但是这就使得聚合的意义不大。
补充
GCN的基本思路：对于每个节点，我们从它的所有邻居节点处获取其特征信息，当然也包括它自身的特征。假设我们使用average()函数。我们将对所有的节点进行同样的操作。最后，我们将这些计算得到的平均值输入到神经网络中。
其实模型在我们上面的第三个方案中已经清楚的讲明了，不过还有一点：为什么叫做图卷积神经网络？它和图像的卷积有什么关系吗？在一些人眼中，关系其实是并不大的，有一点比较相似的地方是，用到了相邻的节点的信息（在图像中是像素）而且会有类似权重一样的东西。
实验
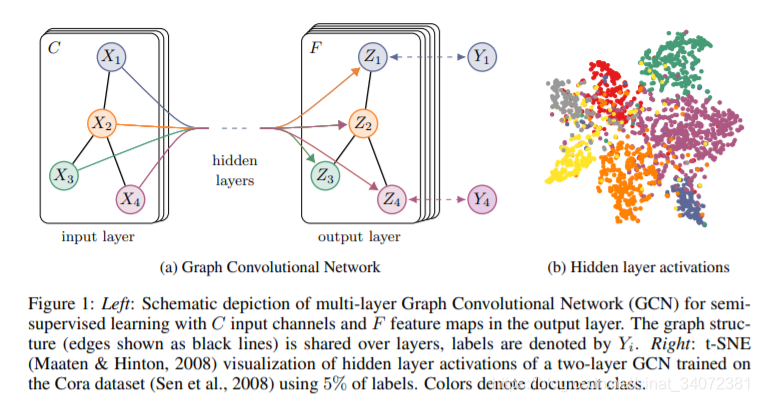
我们有一个多分类问题，有10个类。在第2层有了10个维度的向量后，我们将这些向量通过一个softmax函数进行预测。
\[Z=f(X,A)=\text{softmax}(\hat A\ \text{ReLU}(\hat AXW^{(0)}) W^{(1)}),\quad \hat A=\tilde{D}^{-{1}/{2}} \tilde{A} \tilde{D}^{-{1}/{2}}\]
Loss函数的计算方法很简单，就是通过对所有有标签的例子的交叉熵误差来计算，其中$Y_{l}$是有标签的节点的集合。
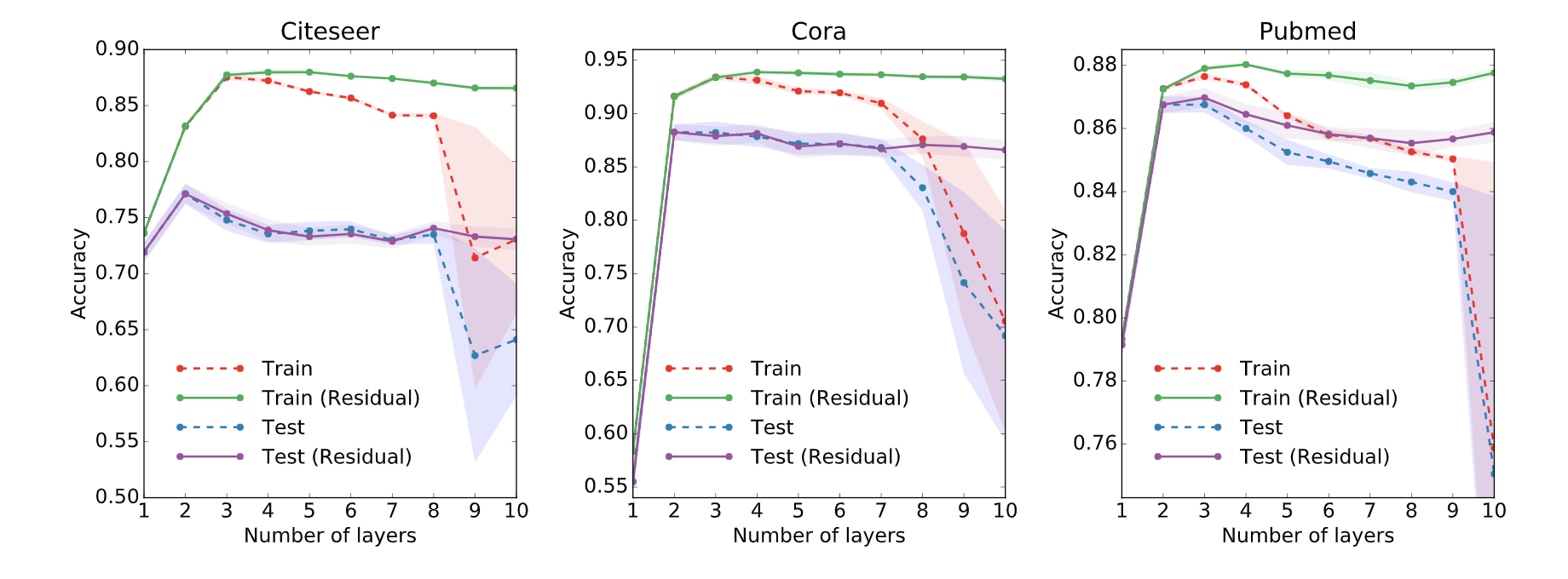
\[\mathcal{L}=-\sum_{l \in \mathcal{Y}_{L}} \sum_{f=1}^{F} Y_{l f} \ln Z_{l f}\]在论文中，作者还分别对浅层和深层的GCN进行了一些实验。在下图中，我们可以看到，使用2层或3层的模型可以得到最好的结果。此外，对于深层的GCN（超过7层），反而往往得到不好的性能（虚线蓝色）。一种解决方案是借助隐藏层之间的残余连接（紫色线）。
