NID任务思考
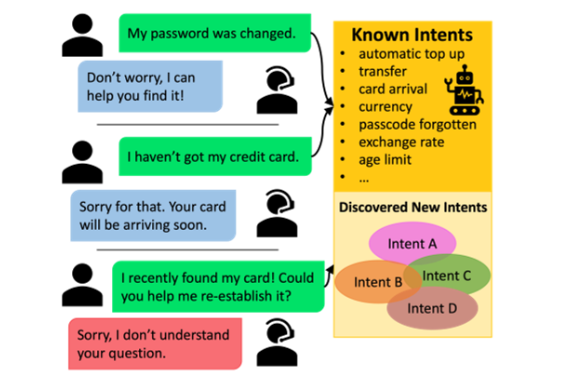
新意图发现(New Intent Discovery,NID)是在部署实际对话系统时面临的重要问题,它在半监督语料库上训练意图分类器,其中未标记的用户话语包含已知和新颖意图。应当如何设计半监督学习算法?
数据集-CLINC150
该数据集用于评估意图分类系统在存在“超出范围”查询的情况下的性能。 “超出范围”是指不属于任何系统支持的意图类的查询。
训练集有1.8W个文本-标签对,测试集和dev集有2250个。文本-标签对的样例如下:
1
2
3
text label
give me my income income
can we talk in french change_language
如果要做半监督任务,可以在保留一部分标签的情况下,把其他标签遮盖掉喂给模型训练。
聚类评价指标:
- 准确率(ACC):通过匈牙利算法(后文将介绍)匹配预测和真实标签后,计算正确聚类的比例。
- 归一化互信息(Normalized Mutual Information,NMI)。度量两个聚类结果的相近程度,通常是将聚类结果和真实标签进行比较相似程度,值域是[ 0 , 1 ],值越高表示两个聚类结果越相似。归一化是指将两个聚类结果的相似性值 定量到0~1之间。
- 调整兰德指数(adjustedRand index,ARI),通过计算在真实标签和聚类结果中被分配在相同或不同类簇的样本对的个数来进行聚类有效性的评价, 取值范围为 [-1,1],值越大意味着聚类结果与真实情况越吻合。
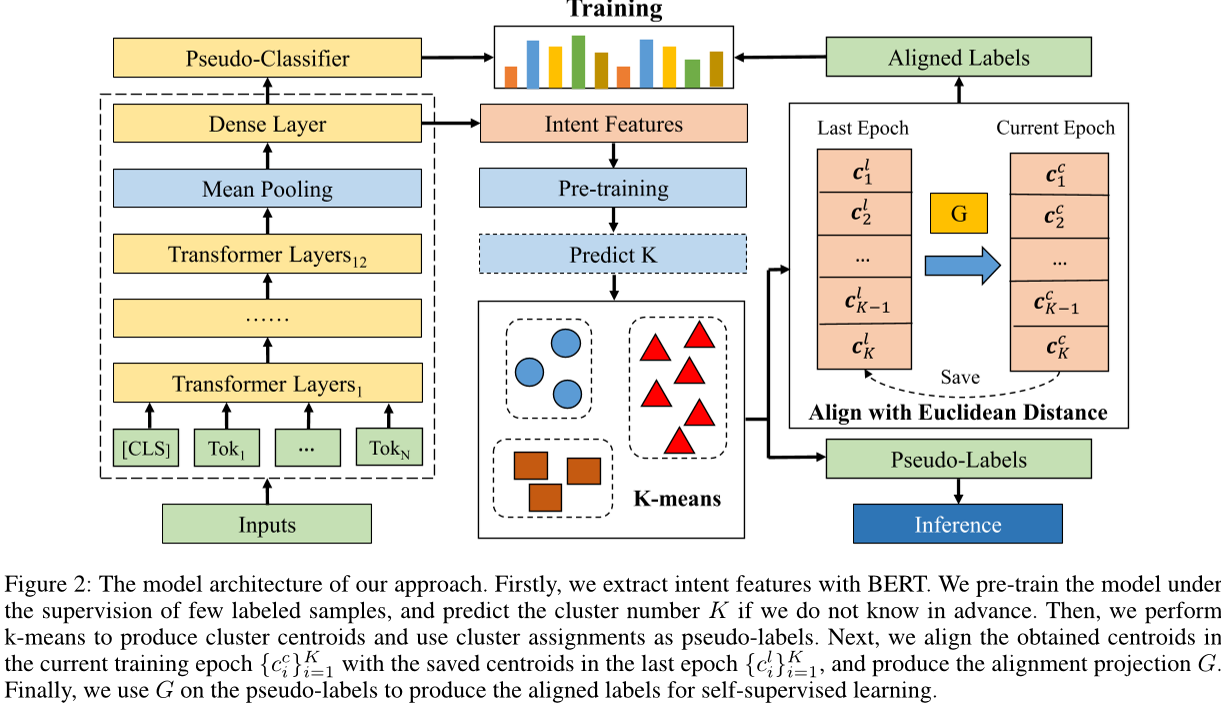
Deep Aligned Clustering
参考:Discovering New Intents with Deep Aligned Clustering
重要步骤:
- (被MTP-CLNN和GeoID使用)使用预训练 BERT 模型在 softmax 损失的指导下,在有限标记的数据上有监督训练
- 拿预训练好的模型提取特征,再拿这些特征使用KMeans聚类得到伪标签
- (被GeoID使用)在每个训练时期,k-means 的索引会随机重排,因此在每个训练时期之前必须重新初始化分类器参数。因此,提出了一种对齐策略来解决分配不一致的问题
- 再拿这些对齐的伪标签去做普通的基于BERT的分类任务
预训练的 BERT 模型
我们将第 i 句输入句子 \(s_i\) 提供给 BERT,并从最后一个隐藏层获取所有标记嵌入,然后应用平均池化以获得平均句子特征表示 \(z_i\),其中 CLS 就是 BERT 中非常有特色的文本分类向量。
\[z_i=\text{mean-pooling}([CLS,T_1,...,T_M])\]为了进一步增强特征提取能力,添加了一个密集层 h 来获得意图特征表示 \(\boldsymbol{I}_i\)
\[\boldsymbol{I}_i = h(z_i)=\sigma(W_h z_i+b_h)\]1
2
encoded_layer_12, pooled_output = self.bert(input_ids, token_type_ids, attention_mask, output_all_encoded_layers = False)
pooled_output = self.dense(encoded_layer_12.mean(dim = 1)) # 密集层
关于预训练,具体来说,以有限的标记的数据作为数据集,在交叉熵损失的指导下学习特征表示。
1
loss = nn.CrossEntropyLoss()(logits, labels)
预训练后,我们删除分类器,并在随后的无监督聚类过程中使用其余网络作为特征提取器。
深度对齐聚类
在预训练模型中提取所有训练数据的意图特征之后,可以使用标准聚类算法 K-Means 来学习最佳簇中心矩阵 \(\boldsymbol{C}\) 和簇分配 \(\{y_{i}\}_{i=1}^N\)
然而,在每个训练 epoch,k-means 的索引会随机重排,因此,我们提出了一种对齐策略来解决分配不一致的问题。
我们将这个问题转化为质心对齐。虽然意图表示不断更新,但相似的意图仍然分布在附近的位置。质心在其簇中综合了所有类似的意图示例,因此更具稳定性,并且更适合指导对齐过程。我们假设连续训练时期的质心在欧几里得空间中相对稳定分布,并使用匈牙利算法(hungarian algorithm)获得最佳映射 G:
\[\boldsymbol{C}^c=G(\boldsymbol{C}^l)\]其中 \(\boldsymbol{C}^c\) 和 \(\boldsymbol{C}^l\) 分别表示当前训练周期和前一个训练周期的质心矩阵。
1
2
3
4
5
6
7
8
9
10
11
12
13
# 获得最佳映射 G
from scipy.optimize import linear_sum_assignment # 匈牙利算法
old_centroids = self.centroids.cpu().numpy() # 旧质心
new_centroids = km.cluster_centers_ # 新质心
# DistanceMatrix[i][j]表示第i个旧中心和第j个新中心之间的欧氏距离
# 我们想要距离小的新旧中心匹配到一起
DistanceMatrix = np.linalg.norm(old_centroids[:,np.newaxis,:]-new_centroids[np.newaxis,:,:],axis=2)
# row_ind[i]表示第i个旧中心和第row_ind[i]个新中心匹配
# col_ind[i]表示第i个新中心和第col_ind[i]个旧中心匹配
row_ind, col_ind = linear_sum_assignment(DistanceMatrix) # 匈牙利算法
然后,我们使用 G(·) 计算对齐的伪标签 \(y^{align}\)
\[y^{align} = G^{-1}(y^c)\]\(G^{-1}\) 表示 G 的逆映射,\(y^c\) 表示当前训练周期中的伪标签。
1
2
3
4
5
6
alignment_labels = list(col_ind)
for i in range(self.num_labels):
label = alignment_labels[i]
self.centroids[i] = new_centroids[label]
pseudo2label = {label:i for i,label in enumerate(alignment_labels)}
pseudo_labels = np.array([pseudo2label[label] for label in km.labels_])
剩下的就简单了!在更新完伪标签后,剩下的就是普通的基于BERT的分类任务。训练好模型后,拿模型生成的语句特征去做K均值聚类看结果。
Hungarian Algorithm
简要介绍一下匈牙利算法,它要解决分配问题,例子如下:
你有三个工人:吉姆,史提夫和艾伦。 你需要其中一个清洁浴室,另一个打扫地板,第三个洗窗,但他们每个人对各项任务要求不同数目数量的钱。 以最低成本的分配工作的方式是什么?
| 清洁浴室 | 打扫地板 | 洗窗 | |
|---|---|---|---|
| 吉姆 | 2 | 3 | 3 |
| 史提夫 | 3 | 2 | 3 |
| 艾伦 | 3 | 3 | 2 |
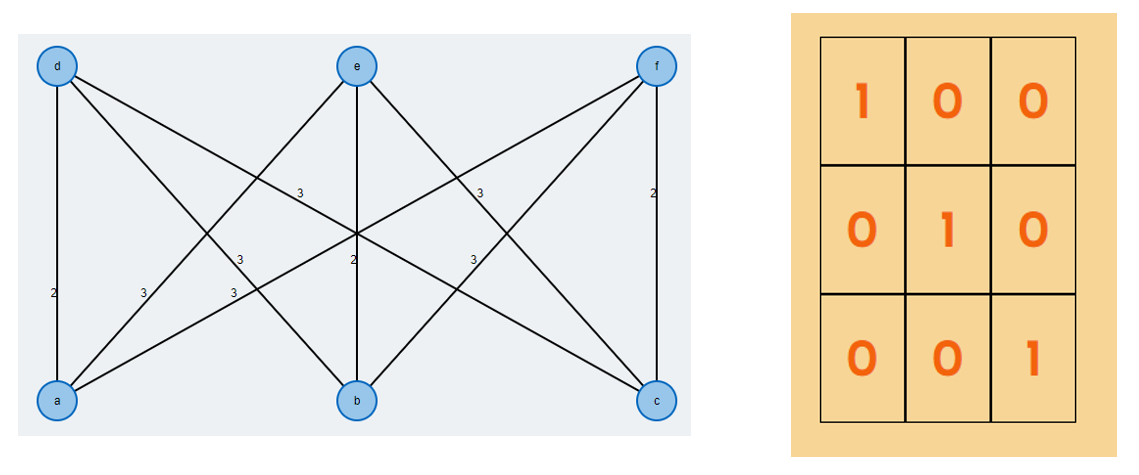
如果用二分图来阐述该问题可以更容易描述这个算法。对于一个有 \(n\) 个工人节点(\(S\))与 \(n\) 个工作节点(\(T\))的完全二分图 \(G=(S\cup T,E)\),每条边都有 \(c(i,j)\) 的非负成本。我们要找到最低成本的完美匹配。
对与上面分配工作例子,对应二分图如下图左,匈牙利算法能将成本矩阵转化为下图右的形式,并给出最低成本为6美元:
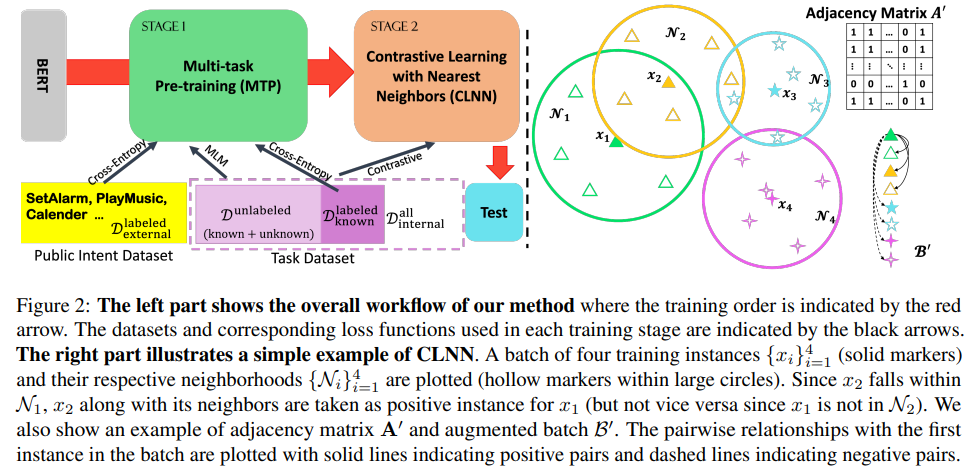
MTP-CLNN
参考:New Intent Discovery with Pre-training and Contrastive Learning
这个名字来源于这篇工作的两个贡献:Multi-task Pre-training (MTP)和Contrastive Learning with Nearest Neighbors (CLNN)
重要步骤:
- (被GeoID使用)使用预训练的 BERT 模型,使用外部标记数据上的交叉熵损失和当前域中所有可用数据上的遮蔽语言建模 (MLM) 损失,进一步预训练模型。
- (被GeoID使用)构造对比学习损失函数,进一步训练模型,不使用伪标签,而是利用嵌入空间中的接近性来拉近相似实例的距离,推远不同实例的距离,从而获得更紧凑的聚类。
多任务预训练
使用预训练的 BERT 编码器初始化模型,多任务预训练包括:
- 使用了来自多个领域的外部公共意图数据集,通过交叉熵损失训练。
- 使用当前域中所有可用的数据(标记或未标记),通过遮蔽语言建模 (MLM) 损失训练。
- (对于半监督任务,也可以使用当前域中已标记数据,通过交叉熵损失训练)
1
2
3
4
5
6
# 为MLM任务准备输入/标签:80% MASK,10% 随机,10% 原始
mask_ids, mask_lb = mask_tokens(X_mlm['input_ids'].cpu(), tokenizer)
X_mlm["input_ids"] = mask_ids.to(self.device)
loss_src = self.model.loss_ce(logits, label_ids) # 交叉熵损失
loss_mlm = self.model.mlmForward(X_mlm, mask_lb.to(self.device)) # MLM损失
lossTOT = loss_src + loss_mlm # 总损失
最近邻对比学习
具体来说,首先使用来自第一阶段的预训练模型对语句进行编码。然后,对于每个语句片段 \(x_i\),在嵌入空间中使用内积作为距离度量来查找其前 K 个最近邻居,从而形成一个邻域 \(\mathcal{N}_i\)(其中的语句片段应与 \(x_i\) 共享相似的意图)
1
2
3
4
5
6
7
8
def get_neighbor_inds(self, args, data):
# 一个工具类,封装了加权KNN算法、KNN算法、最近邻算法等
memory_bank = MemoryBank(len(data.train_semi_dataset), args.feat_dim, len(data.all_label_list), 0.1)
# 使用提供的模型提取特征,并将这些特征添加到memory_bank中
fill_memory_bank(data.train_semi_dataloader, self.model, memory_bank)
# 查找其前 K 个最近邻居
indices = memory_bank.mine_nearest_neighbors(args.topk, calculate_accuracy=False)
return indices # 邻居的索引
在训练过程中,我们从语句批次 \(\mathcal{B}=\{x_i\}_{i=1}^M\) 中随机采样一个 mini-batch。对于批次 B 中的每个语句 \(x_i\),我们从其邻域 \(\mathcal{N}_i\) 中均匀采样一个邻居 \(x_i'\)
1
2
3
4
5
6
7
def __getitem__(self, index):
# 从原始数据集中获取索引对应的样本(称为“锚点”样本)
anchor = list(self.dataset.__getitem__(index))
# 从该样本的最近邻索引中随机选择一个索引,并获取对应的邻居样本
neighbor_index = np.random.choice(self.indices[index], 1)[0]
neighbor = self.dataset.__getitem__(neighbor_index)
然后,我们使用数据增强为 \(x_i\) 和 \(x_i'\) 分别生成 \(\tilde{x}_i\) 和 \(\tilde{x}_i'\),它们形成了一个正样本对(这一节的小标题为:对比学习)。
因为我们观察到一个语句的目的可以通过一小部分单词来表达,例如 “suggest restaurant” 和 “book a flight”。虽然很难为未标记的语句识别关键字,但随机用一些来自库中的随机token替换其中的一小部分token不会影响意图语义。这种方法在我们的实验中效果很好。
1
2
X_an = {"input_ids":self.generator.random_token_replace(anchor[0].cpu()).to(self.device), "attention_mask":anchor[1], "token_type_ids":anchor[2]} # 增强后的x_i
X_ng = {"input_ids":self.generator.random_token_replace(neighbor[0].cpu()).to(self.device), "attention_mask":neighbor[1], "token_type_ids":neighbor[2]} # 增强后的x_i'
在获得包含所有生成样本的增强批次 \(\mathcal{B}'=\{\tilde{x}_i,\tilde{x}_i'\}_{i=1}^M\) 之后,为了计算对比损失,我们为 \(\mathcal{B}'\) 构建了一个邻接矩阵 \(\boldsymbol{A'}\),这是一个形状为 (2M×2M) 的二进制矩阵,其中 1 表示正关系(即要么是邻居,要么在半监督 NID 中具有相同的标签),0 表示负关系。
1
2
3
4
5
6
7
8
adj = torch.zeros(inds.shape[0], inds.shape[0]) # 邻接矩阵
for b1, n in enumerate(neighbors):
adj[b1][b1] = 1
for b2, j in enumerate(inds):
if j in n:
adj[b1][b2] = 1 # if in neighbors
if (targets[b1] == targets[b2]) and (targets[b1]>0) and (targets[b2]>0):
adj[b1][b2] = 1 # if same labels
通过预训练好的模型,我们可以拿到句子的嵌入 \(h_i\),损失函数如下:
\[l_i = -\frac{1}{|\mathcal{C}_i|} \sum_{j \in \mathcal{C}_i} \log \frac{\exp(\text{sim}(\tilde{h}_i, \tilde{h}_j) / \tau)}{\sum_{k \neq i}^{2M} \exp(\text{sim}(\tilde{h}_i, \tilde{h}_k) / \tau)}\] \[\mathcal{L}_{\text{stg2}} = \frac{1}{2M} \sum_{i=1}^{2M} l_i\]\(l_i\)公式表示的是对比损失的一个推广形式。整个损失函数 \(\mathcal{L}_{\text{stg2}}\) 是所有样本损失的平均值。
\(\mathcal{C}_i\) 表示与样本 \(\tilde{x}_i\) 有正样本集合。加上绝对值符号就是集合中正样本的数量
\(\tau\) 是温度参数,控制分布的平滑度。这个参数在很多大模型对话系统中我们都看到过了
sim是一个在一对归一化特征向量上定义的相似度函数,比如点积
用一个类似 softmax 的公式来计算对比损失,第一眼看上去有点奇怪,但是想一想,模型越好,正相关关系的样本相似度越大越突出,\(l_i\)公式分子越大,加负号,损失就越小,这是合理的。
1
2
3
4
5
6
7
8
# 之前的邻接矩阵A’在这里充当mask
logits = torch.div(
torch.matmul(anchor_feature, contrast_feature.T),
self.temperature
) # 分母,计算锚点特征和所有对比特征之间的点积
exp_logits = torch.exp(logits) * logits_mask # 分子,只保留 mask 中为1的部分,即正样本
log_prob = logits - torch.log(exp_logits.sum(1, keepdim=True)) # 分子分母与负log计算
mean_log_prob_pos = (mask * log_prob).sum(1) / mask.sum(1) # 求和以及求均值
剩下的就简单了!在使用对比损失训练好模型后,剩下的就是拿模型生成的语句特征去做K均值聚类看结果。
GeoID
参考:Learning Geometry-Aware Representations for New Intent Discovery
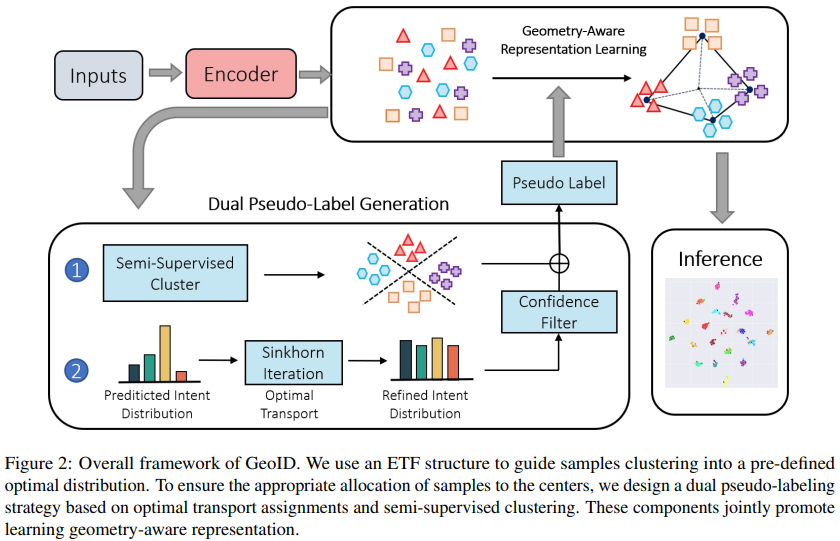
Geometry-aware representation learning framework for NID(GeoID),基于几何信息的表示学习框架。
“几何”这个名字来源于神经崩塌(neural collapse,NC)现象,在理想条件下,随着分类器在收敛方向上进行训练,特定类别的最终层特征会逐渐收敛到该类别内的平均值。这些平均值随后倾向于定位在最大角度距离上的超球面上,即正交等角紧框架(simplex equiangular tight frame,simplex ETF)
简而言之,神经崩塌现象提供了一个结构,可以将特征分布到最大角度距离上的超球面上。而在聚类任务中,不同的类要相互远离,目标是一样的。如下图左。
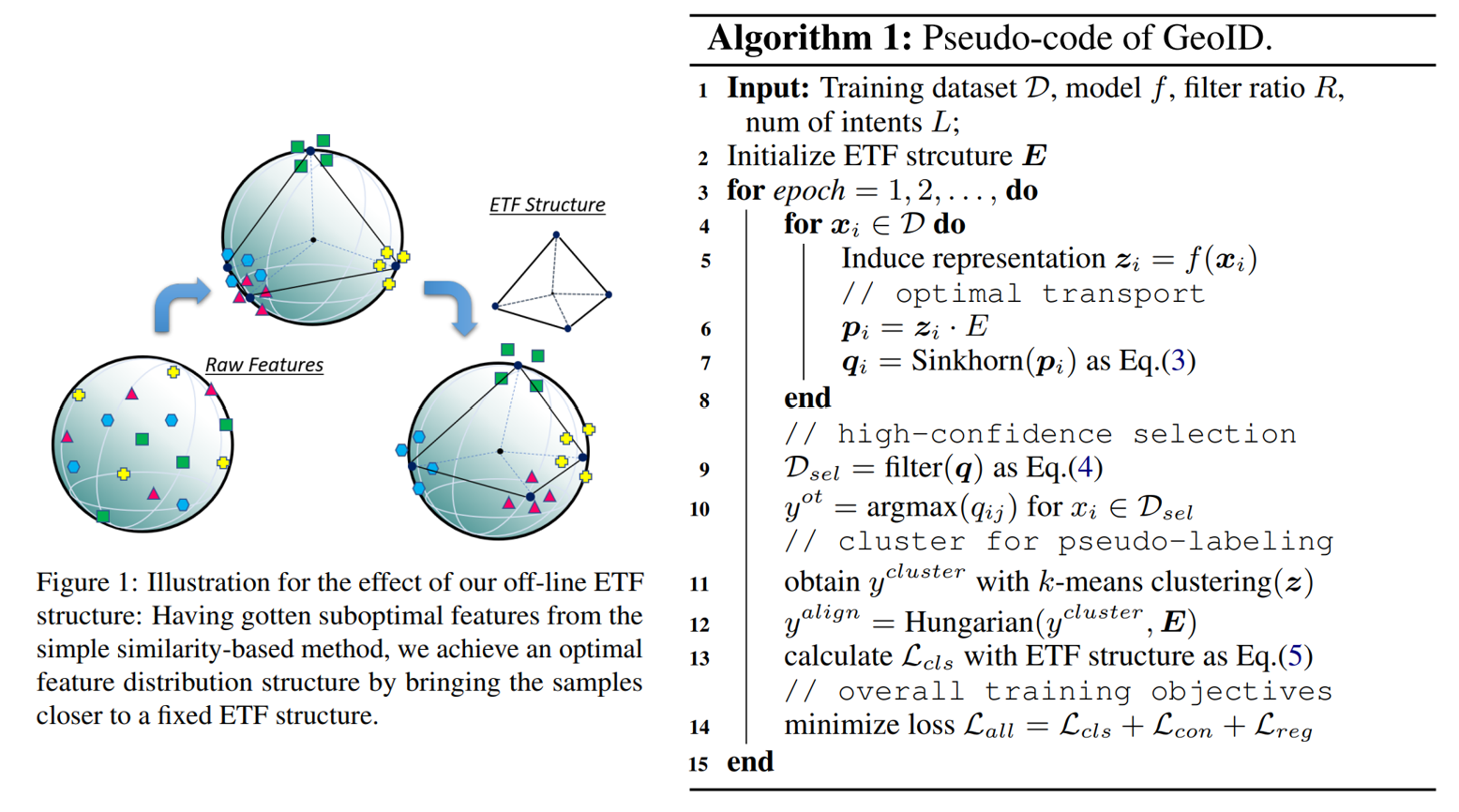
上图右是 GeoID 算法伪代码,之后的介绍会按照伪代码的顺序展开。
神经崩塌
什么是神经崩塌现象?举个例子,一个神经网络需要对猫、狗和鸟的图片进行分类。最初,网络不能很好地区分这些动物,并且它用来表示每个类别的特征可能会显着重叠。
然而,随着训练的进展,网络开始更好地识别猫、狗和鸟类的独特特征。一个类中的特征(例如,所有猫)变得更加相似(集中在平均值周围),使得网络更容易正确地对它们进行分类。
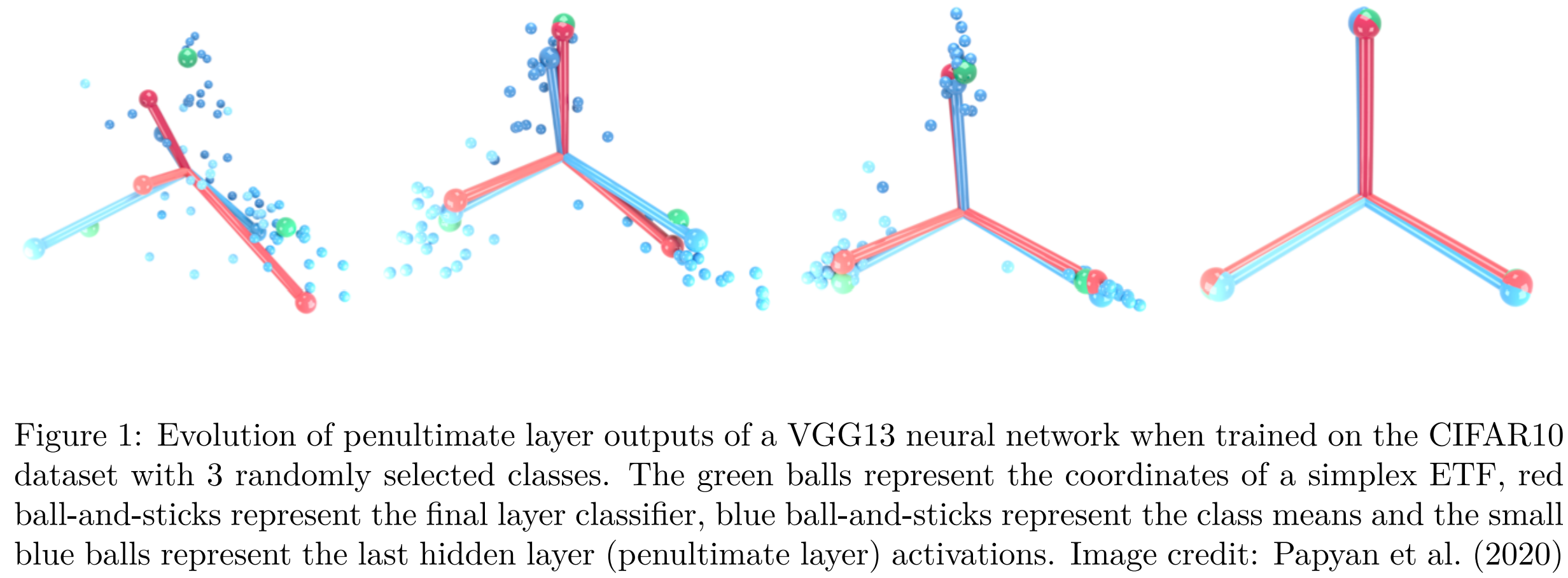
可视化解释:
- 红线(最终层分类器)表示网络末端的分类器,模型使用这些决策边界进行分类。
- 蓝线(类平均值)代表最后一个隐藏层中每个类的激活的平均值(平均点)。
- 小蓝球(最后一个隐藏层的激活值):这些是最后一个隐藏层中样本的单独激活(特征向量)。它们显示了每个类别的数据点如何围绕类别均值分布、紧密聚集。
- 绿球(Simplex ETF):绿色代表 Simplex ETF 的坐标,一种由于神经崩塌现象而导致该类别趋于近似的几何结构。
Simplex ETF 是一种特殊的模式,它在其覆盖的空间中均匀分布,形成一个在所有方向上等距的简单形状。现在,对于三个类别,理想情况下是一个等边三角形,表示特征空间中每个类别平均值之间的距离和角度相等。
最初,每个类别的激活值可能是分散的,但随着训练的进行,网络会经历这种“神经崩塌”。类均值(蓝线)向Simplex ETF(绿球)的顶点汇聚,并且各个激活值(小蓝球)紧密聚集在这些均值周围。分类器(红线)相应地进行调整,以准确地分离这些不同的类簇。
计算 Simplex ETF
假设向量空间为 \(d\) 维。当\(d \geq L−1\) 时,我们可以始终得到一组长度相等且最大角度一致的\(d\) 维嵌入向量 \(\boldsymbol{E}=[e^∗_1,..., e^∗_L]\) 来构造一个 Simplex ETF
\[\boldsymbol{E}=\sqrt{\frac{L}{L-1}}\text{U}(\boldsymbol{I}_L-\frac{1}{L}\boldsymbol{1}_L \boldsymbol{1}_L^\mathsf{T})\]其中 \(\boldsymbol{I}_L\) 是单位矩阵,\(\boldsymbol{1}_L\) 是一个全为 1 的向量,U 是旋转矩阵。在训练过程中,我们保持 \(\boldsymbol{E}\) 固定。
1
2
3
4
5
# 随机正交矩阵,表示旋转,(feat_in, num_classes)
P = self.generate_random_orthogonal_matrix(feat_in, num_classes,try_assert)
I = torch.eye(num_classes) # eye 生成单位矩阵,(num_classes, num_classes)
one = torch.ones(num_classes, num_classes) # (num_classes, num_classes)
M = np.sqrt(num_classes / (num_classes-1)) * torch.matmul(P, I-((1/num_classes) * one))
现在,我们构造好了一个 Simplex ETF,然后我们想要使 BERT 计算出的语句特征 \(z_i\) 靠近这些中心,具体来说,通过优化下述交叉熵损失来靠近:
\[\mathcal{L}_{etf}(x_i, \hat{y}_i) = -\log \frac{\exp(z_i^\top \cdot e^*_{\hat{y}_i})}{\sum_{l=1}^{L} \exp(z_i^\top \cdot e^*_l)}\]1
2
3
4
5
cls_embed = outputs.hidden_states[-1][:,0] # 提取[CLS]的特征
pooled_output=self.head(cls_embed) # 经过一个全连接层,得到z_i,语句 x_i 的特征表示
feat_norm = self.classifier_new(pooled_output) # 归一化
cur_M = self.classifier_new.ori_M.cuda() # ETF预分配中心E
logit = torch.matmul(feat_norm, cur_M) # zi 与 e 的积
最佳运输
在机器学习中,我们经常在想要计算如何将一种分布转换为另一种分布的最佳传输方法。例如,我们可能关心的是计算得到两个概率分布之间的传输。
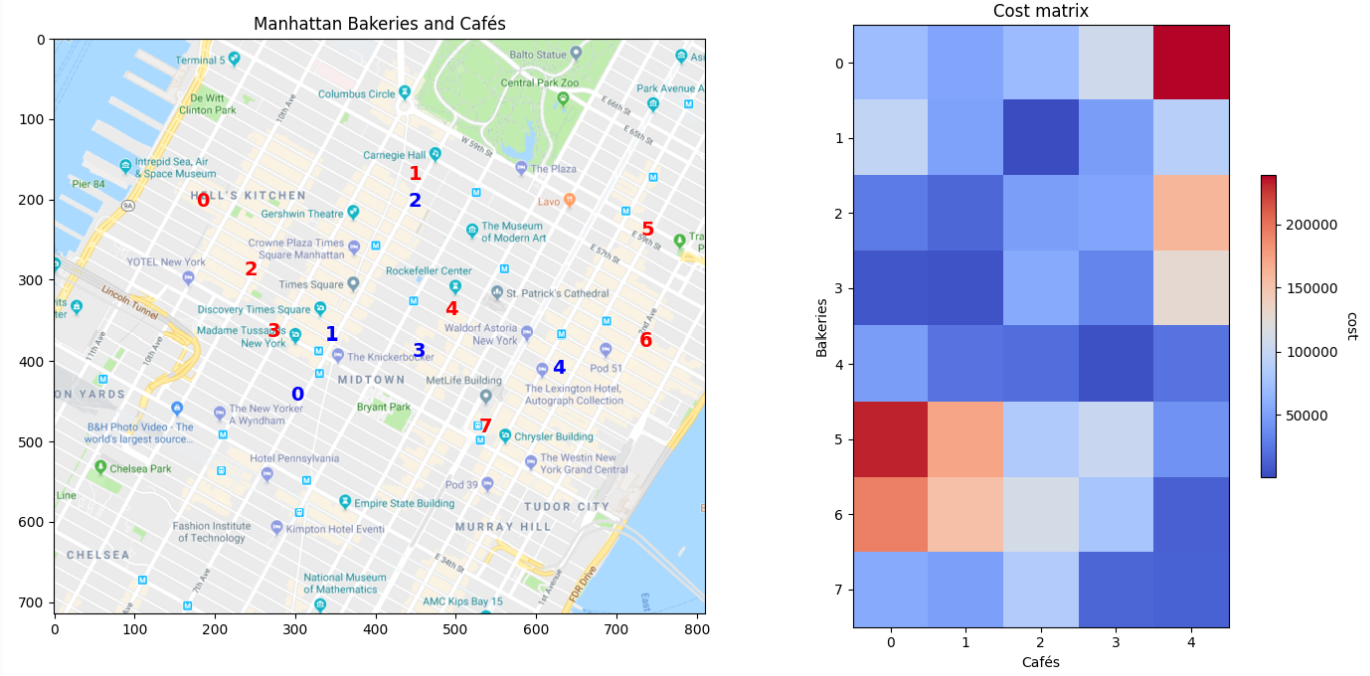
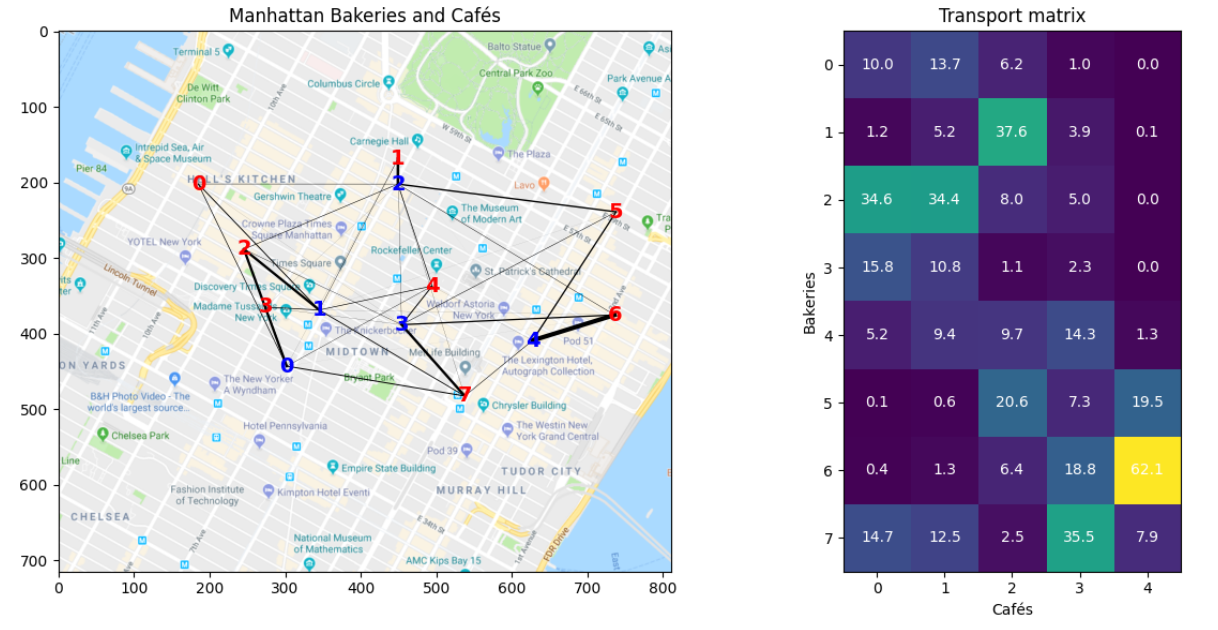
在现实世界中,假设我们想解决将面包从多个面包店运输到一个城市的咖啡馆。我们在地图上标记了面包店(红色)和咖啡馆(蓝色),并得到运输成本矩阵:
我们希望有一个算法,可以帮助我们得到运输矩阵,即从每个面包店运输到每个咖啡馆的面包的数量,并且成本最小:
用数学公式抽象这个目标,即:
\[\boldsymbol{Q} = \max_{\boldsymbol{Q} \in \Delta} \text{Tr}(\boldsymbol{Q}^\top \boldsymbol{P}) = \sum_{i=1}^{b} \sum_{j=1}^{L} q_{ij}^\top p_{ij}\]- Q 是一个矩阵,表示运输计划
- \(\Delta\) 表示所有满足约束条件的运输计划矩阵的集合
- \[p_{i} = \text{softmax}(z_i^\top \cdot \boldsymbol{E})\]
- \(q_{ij}\) 是第 i 个样本伪标签的第 j 个元素
- 矩阵 \(Q^\top P\) 的迹 Tr,表示运输计划的总成本
- 通常最优运输问题是最小化总成本,不过在我们的半监督任务中,我们要搜索一个最优的标签分配 \(\boldsymbol{Q}=[q_1,…,q_b]\) ,使其接近当前预测P,因此我们的目标是最大化这个总成本
约束条件 (Constraints):
\[\text{s.t. } \Delta = \{ [q_{ij}]_{L \times b} \ | \ Q \mathbf{1}_b = r, Q^\top \mathbf{1}_L = c \}\]- \(Q \mathbf{1}_b = r\) : 确保每个源的总供给量等于供给向量 r 中对应的元素,其中 \(\mathbf{1}_b\) 是一个全 1 向量,长度为 b
- \(Q^\top \mathbf{1}_L = c\) :确保每个目标 j 的总需求量等于需求向量 c 中对应的元素
Sinkhorn-Knopp
Sinkhorn-Knopp 算法可以通过计算得到优化后的标签分布结果:
不过实现方式有所不同,首先计算得到成本矩阵:
\[M=\text{exp}\left(\frac{P}{\epsilon}\right)\]1
q = logits / self.epsilon
令 r 表示先验类别分布, c 表示批处理中 b 个样本被均匀采样:
\[r=\frac{1}{L}\mathbf{1}_L, c=\frac{1}{b}\mathbf{1}_b\]1
2
r = torch.ones(Q.shape[0]).cuda(non_blocking=True) / Q.shape[0]
c = torch.ones(Q.shape[1]).cuda(non_blocking=True) / Q.shape[1]
多次迭代,公式中 \(./\) 代表按元素除:
\[\mu \leftarrow r./M v, v \leftarrow c./M^\top \mu\]1
2
3
4
5
6
7
for it in range(self.num_iters):
u = torch.sum(Q, dim=1)
u = r / u # 计算行标准化因子
u = shoot_infs(u) # 去掉 inf 值
Q *= u.unsqueeze(1) # 按行标准化
Q *= (c / torch.sum(Q, dim=0)).unsqueeze(0) # 按列标准化
return (Q / torch.sum(Q, dim=0, keepdim=True)).t().float()
在实现中,最终标签分布结果 Q 不是一次计算得到的,而是通过多次迭代逐渐得到的,从而实现:
\(Q=M \odot(\mu\cdot v^T)\) 此外的一个细节:如此强大的分配必然会引入大量的噪声。为了缓解标签错误的积累,我们通过高置信度选择过滤伪标记。换句话说,我们在每个聚类中选择了最可靠的样本,并将其用作整个聚类的支点,以引导整个聚类朝向 ETF 中心移动。
1
2
3
4
index_j = np.where(targets_all.cpu().numpy()==j)[0] # 找出所有具有相同标签j的数据点的索引
max_score_j = max_probs_all[index_j] # 获取最大概率
sort_index_j = (-max_score_j).sort()[1].cpu().numpy() # 根据这些数据点的最大概率值进行排序
partition_j = int(len(index_j)*rho_l) # 只选择前rho_l的数据点
聚类策略
在每个训练周期中,通过k均值获得的聚类标签索引被随机打乱,这使得我们很难充分利用聚类结果提供的监督信息。借鉴了 Deep Aligned 的深度对齐聚类方法,见上,这里不再赘述。
损失函数
可以看到,Sinkhorn-Knopp 算法给我们了一份 ot(Optimal Transport) 假标签,k均值也给了我们一份 align 假标签,我们希望同时利用这两份标签,通过交叉熵损失,来指导更好地半监督学习。
\[\mathcal{L}_{cls}=\alpha \mathcal{L}_{etf}(x,y^{ot})+(1-\alpha)\mathcal{L}_{etf}(x,y^{align})\]在开始时,ETF分类器倾向于信任聚类伪标签以避免表示坍塌。随着训练的进行,过滤的OT标签可以逐渐变得更加可靠,并引导数据簇朝向预先定义好的ETF框架移动。与此同时,基于数据驱动的聚类伪标签仍然作为一个适当的正则化项,使剩余的数据与其过滤后的邻居对齐,确保充分利用所有数据。最后,所有的数据样本都紧密地聚集在其相应的中心处,实现了我们所期望的最佳几何分布。
同时使用了来自 MTP-CLNN 的对比学习的损失函数 \(\mathcal{L}_{con}\) 见上,这里不再赘述。
同时使用了来自 MTP-CLNN 的随机标记替换作为数据增强策略,通过骨干网络获得两个表示,\(z_1'\) 和 \(z_2'\) ,以对 x 进行增强。 最后,我们计算两者之间的KL散度作为 \(\mathcal{L}_{reg}\) 正则项
\[\mathcal{L}_{all}=\mathcal{L}_{cls}+\mathcal{L}_{con}+\mathcal{L}_{reg}\]使用大模型
参考:Large Language Models Meet Open-World Intent Discovery and Recognition: An Evaluation of ChatGPT
可以使用大模型来进行 NID 任务,方法包括:
- 直接聚类(Direct clustering,DC):由于 OOD(out-of-domain,域外) 意图发现本质上是一种聚类任务,一个朴素的方法是在不使用任何 IND(in-domain,域内) 先验知识的情况下直接进行聚类。
- 零样本发现(Zero Shot Discovery,ZSD):这种方法提供提示中的IND意图集作为先验知识,但不提供任何IND示例。 它可以用于需要保护用户隐私的情况。
- 少样本发现(Few Shot Discovery,FSD):FSD 为每个 IND 意图提供多个标记示例,希望 ChatGPT 能够从 IND 表演中挖掘领域知识,并将其转移到帮助 OOD 意图聚类。
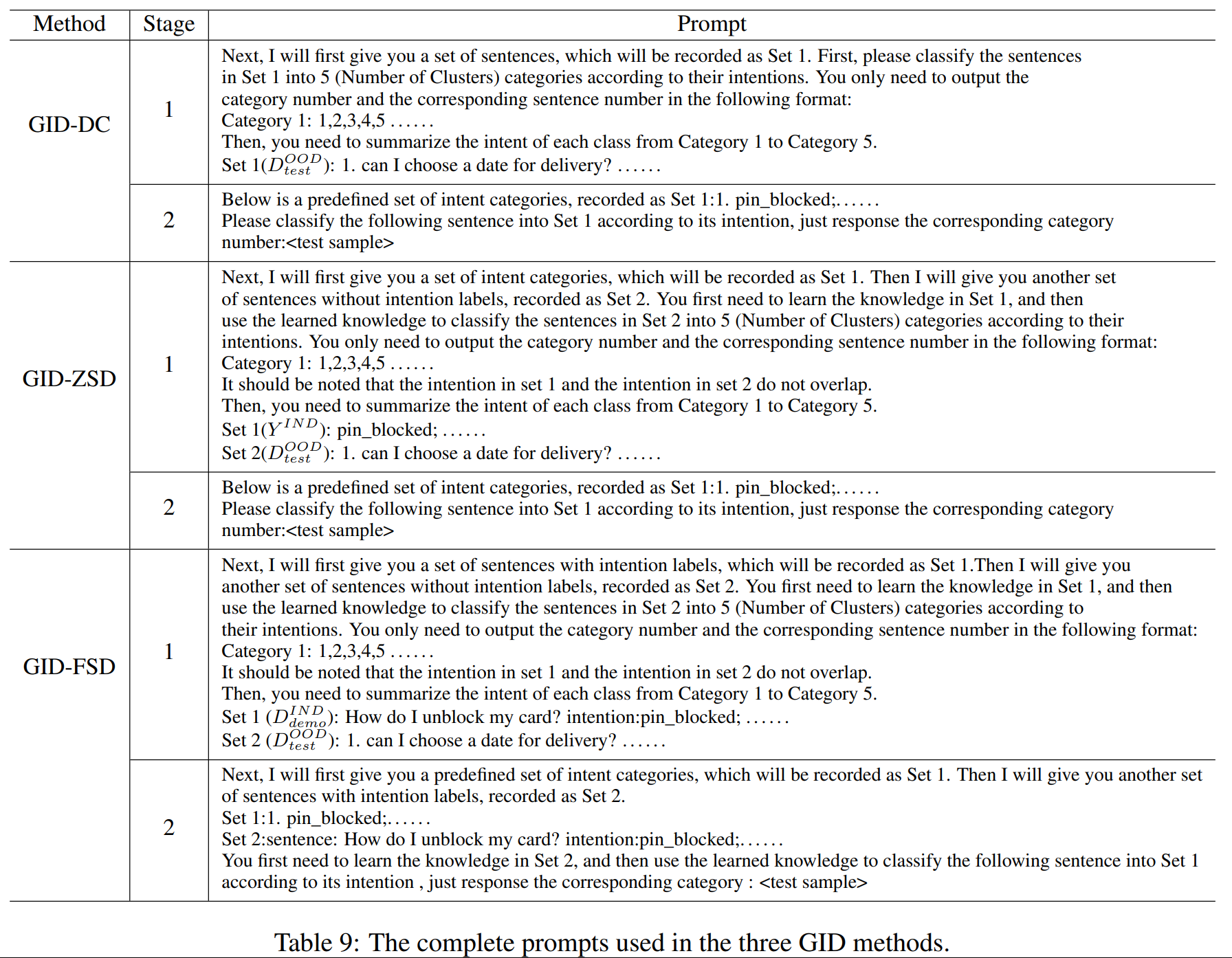
三种方法的提示词格式如下:
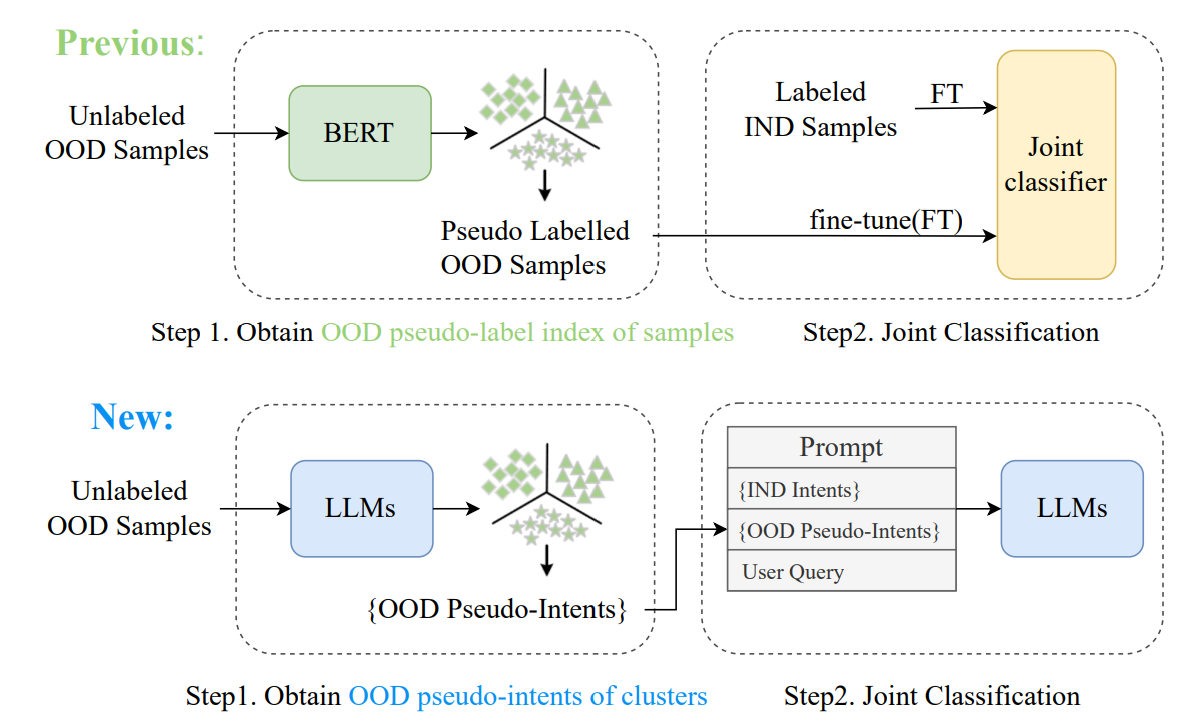
我们甚至可以用之前方法中的伪标签来帮助大模型聚类!下图是传统方法和基于大模型方法的对比:
在第一阶段,我们在 OOD 意图发现提示的基础上添加了生成意图描述的额外的指令,输入到 ChatGPT 中,并获得每个聚类的意图描述。通过聚合这些意图描述,我们获得了伪标签集。
第二阶段,并将伪标签集添加到现有的 IND 意图集中。并设计合适的提示词格式让大模型聚类。提示词格式如下:
GeoID 探索了如何与 LLM 合作完成 NID 任务。LLM在NID任务中的主要挑战在于缺乏先验新颖类,这严重影响了大型模型的上下文学习。为了解决这个问题,GeoID选择靠近中心的语料库来提供新颖类的先验。 在实践中,对于每个新的类别,选择距离类中心最近的 10% 的样本,并以以下形式设计提示:
1
<Prior: labeled samples and selected samples><Cluster Instruction><Response Format><D_test>