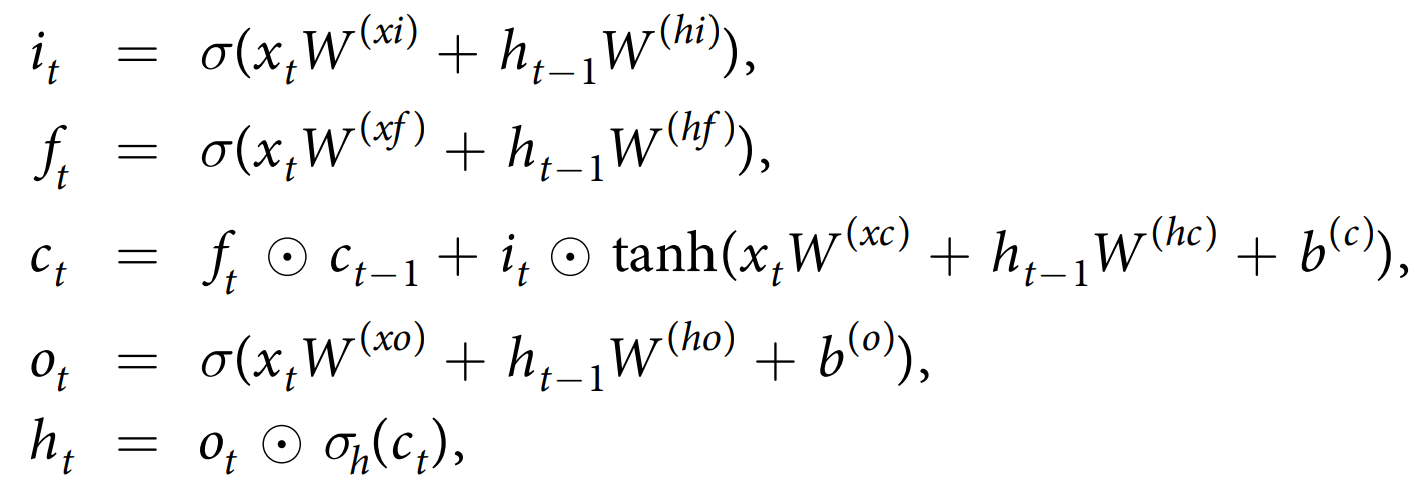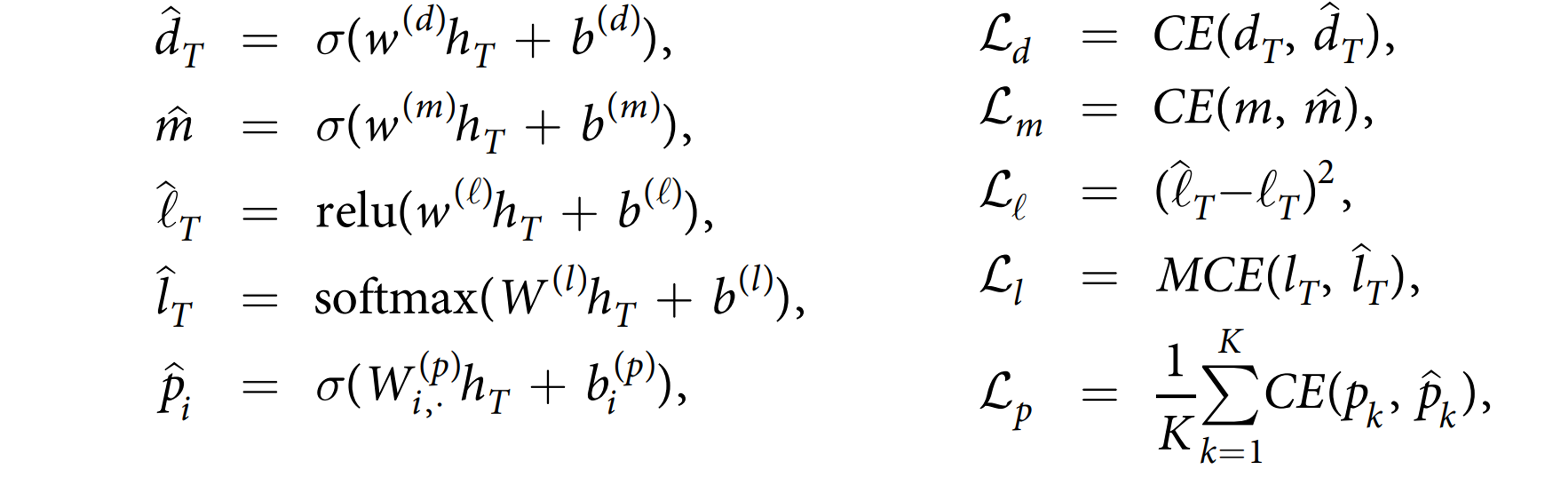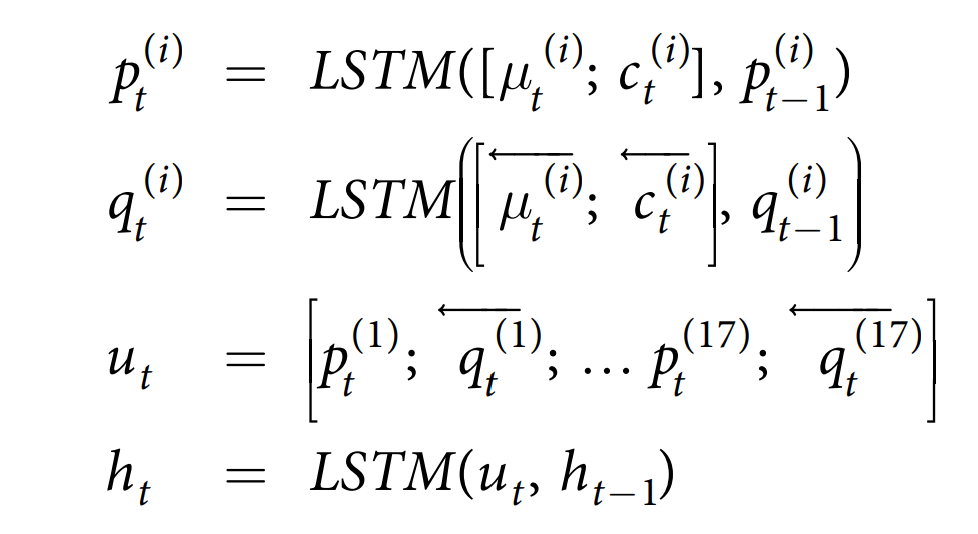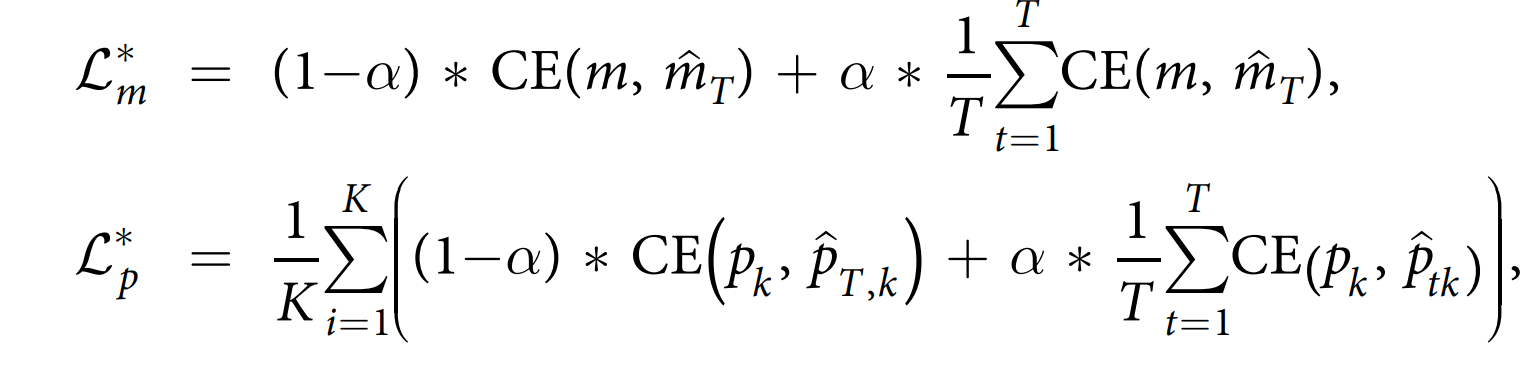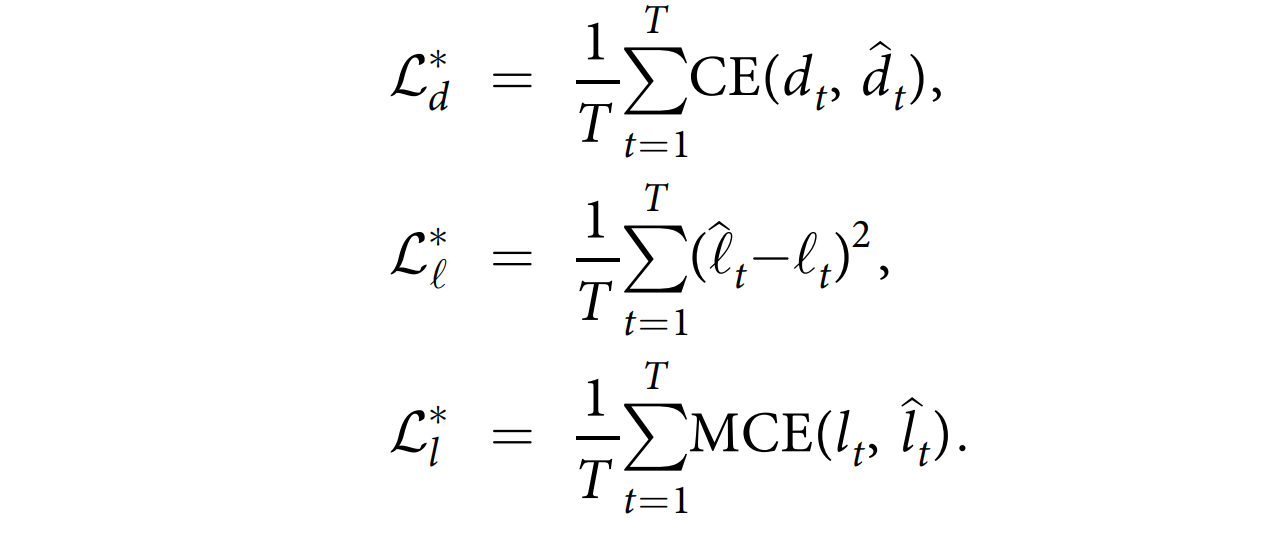Multitask learning and benchmarking with clinical time series data
读论文时间!来自:https://www.nature.com/sdata/
介绍
由于缺乏公开可用的基准数据集,衡量用于医疗保健研究的机器学习进展一直很困难。
为了解决这个问题,我们提出了四个临床预测基准:
- 院内死亡,in-hospital mortality
- 生理衰竭,physiologic decompensation
- 住院时间,length of stay (LOS)
- 表型分类,phenotype classification
使用了来自公共可得的医疗信息Medical Information Mart for Intensive Care (MIMIC-III) 数据库。其中包含来自超过 40,000 名重症监护病房患者的丰富多元时间序列数据,以及用于四个任务的标签。
这些任务不仅在输出类型上有所不同,而且在时间结构上也不同。它们的异质性需要一种能够处理序列数据并建模随时间分布的任务之间相关性的模型解决方案。我们证明了精心设计的递归神经网络能够利用这些相关性来提高多项任务的性能。
相关工作
前馈神经网络在建模住院患者死亡风险时,几乎总是优于逻辑回归和疾病严重程度评分。前馈网络、LSTM 网络 和时序卷积网络 都被用于预测临床时间序列中的诊断代码。
2016 年,首次证明递归神经网络 可以在可变长度的临床时间序列中对数十种急性护理诊断进行分类 。
多任务学习起源于临床预测,一些例子:
- 将表型定义为多标签分类,使用神经网络隐含地捕获隐藏层中的共病性。
- 联合解决多个相关的临床任务,包括预测死亡率和住院时间。
- 用一个卷积神经网络来执行各种自然语言处理任务(词性标注、命名实体识别和语言建模),具有不同的序列结构。
数据集
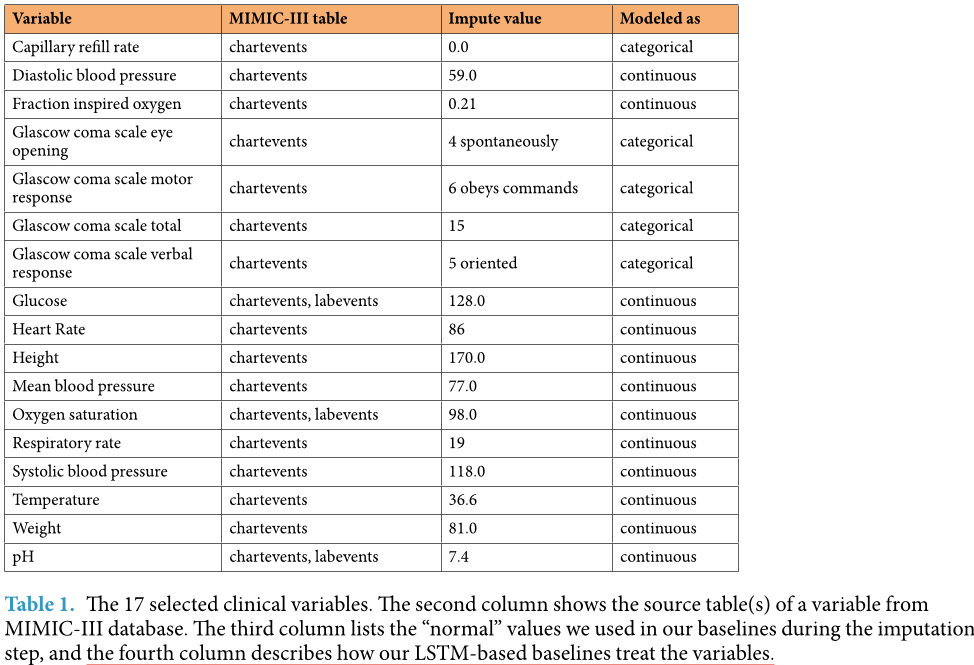
MIMIC-III 数据库中提取了一个子集,其中包含超过 3100 万条临床事件,这些事件对应于下图第一列中的 17 个临床变量。这些事件覆盖了 33,798 名患者在重症监护室 (ICU) 的 42,276 次停留。我们在该子集中定义了四项基准任务:
图片解释:选定的 17 个临床变量。第二列显示了来自 MIMIC-III 数据库中变量的来源表。第三列表出了我们在插补步骤中使用的“正常”值,第四列表出了我们的基于 LSTM 的基线如何处理这些变量。
- 预测医院内死亡率——根据ICU头48小时停留预测院内死亡率。这是一个二元分类任务,曲线下面积(AUC-ROC)是主要指标。
- 代偿失调预测(Decompensation prediction)——预测患者在接下来的24小时内健康状况是否会迅速恶化。这项任务的目标是取代目前医院使用的预警评分系统。这个任务的每个实例都是二元分类问题。同样地,在院内死亡率预测中,主要指标是AUC-ROC。
- 住院时间预测——在每个入住小时预测ICU剩余停留时间。我们将其定义为一个有10个类别/桶的问题(其中一天之内的ICU停留被分为一个类别,第一周的每一天各占7天,一周以上的但少于两周的占一个类别,超过两周的占一个类别)。此任务的主要度量标准是Cohen线性加权Kappa分数。
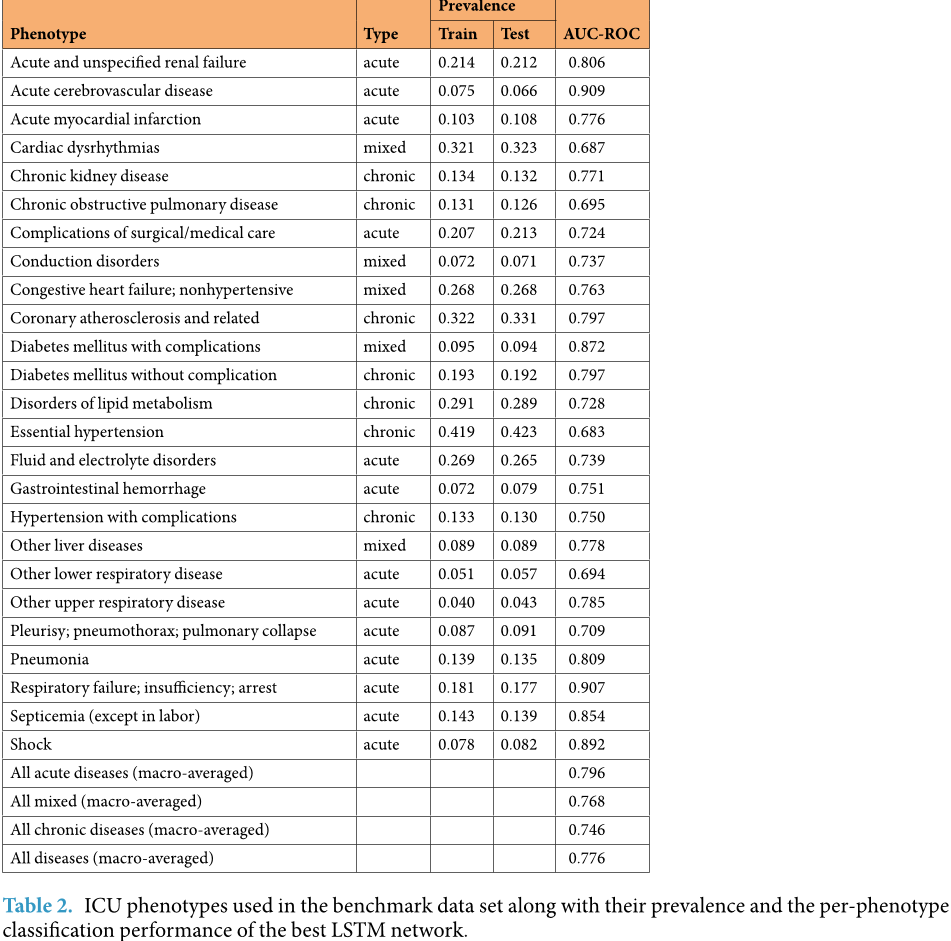
- 表型分类(Phenotype classification)——对给定患者 ICU 检查记录中存在哪些 25 种急性护理条件(如下图)进行分类。这是一个多标签分类问题,宏平均 AUC-ROC 是主要指标。
请注意,我们执行的是“回顾性”表型分类,在预测存在哪些疾病之前,我们会观察完整的重症监护室停留时间。这部分是因为MIMIC-III的局限性:我们的疾病标签来源,即ICD-9代码,没有时间戳,所以我们不能确定患者何时被诊断或首次出现症状。
图片解释:基准数据集中使用的 ICU 现象及其出现率,以及最佳 LSTM 网络针对每种现象的分类性能。
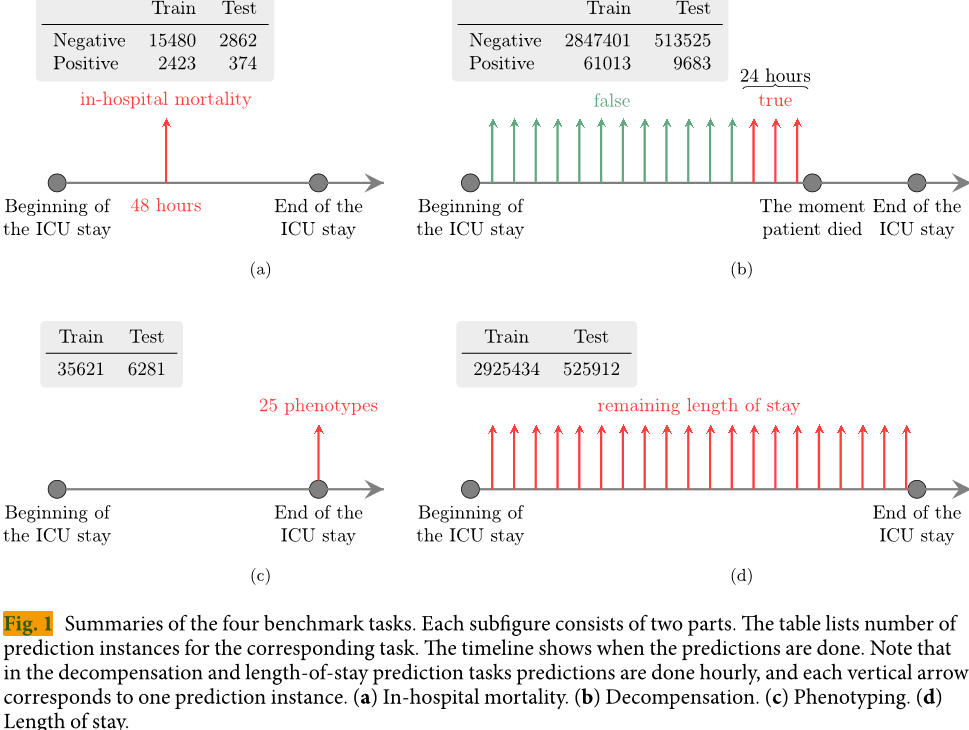
图片解释:四个基准任务的总结。 每个子图包含两部分。 表格列出了每个任务对应的预测实例数量。 时间线显示了预测完成的时间。 注意,在代偿失调和住院时间预测任务中,每小时进行一次预测,每个垂直箭头对应一个预测实例。(A) 住院死亡率。(B) 代偿失调。(C) 分型。(D) 住院时间。
结论
开发了线性回归模型和多个神经架构。我们使用基本的基于 LSTM 的神经网络(标准LSTM)进行实验,并引入其变体(channel-wise LSTM)。
基于LSTM 的模型在所有任务的所有指标上都优于线性模型。
鉴于相对于复杂性而言数据通常规模较小,深度学习对健康数据的有效性仍存在疑问。
我们的结果进一步证明,复杂的架构可以有效地训练非互联网规模的健康数据,虽然像过拟合这样的挑战仍然存在,但可以通过仔细的正则化方案来缓解,包括丢弃法和多任务学习。
实验表明,channel-wise LSTM和多任务训练对几乎所有任务都起到了正则化的作用。
与标准LSTM相比,channel-wise LSTM在所有四项任务中均表现显著优于标准LSTM。
而多任务处理对于除表型外的所有任务都有帮助。我们假设这是因为表型分类本身就是一种多任务问题,并且已经在共享LSTM层以跨越25种不同表型的情况下受益于正则化。
通过添加具有损失加权的更多任务,可能会限制多任务LSTM有效地学习识别单个表型的能力。
请注意,在多任务模型的超参数搜索中,任何一项任务都没有使用零系数。这就是为什么最佳多任务模型有时比单任务模型表现更差的原因。
通道级层和多任务处理的结合也是有用的。channel-wise LSTM的多任务版本在医院死亡率预测和表型分型任务中,显著优于相应的单任务版本。
在衰竭和住院时间预测任务中,我们观察到深度监督带来了显著的改进(除了用于住院时间预测的标准LSTM模型)。在这两项任务中,获胜者都是带深度监督的channel-wise LSTM。
我们展示了使用channel-wise LSTM和学习使用单个神经模型来预测多个任务的优势。
我们的结果表明,表型分类和住院时间预测任务比死亡率和代偿失调预测任务更具挑战性,并需要更大的模型架构。即使是小型的LSTM模型也很容易过拟合后两个问题。
我们注意到,由于MIMIC-III中的数据是在单个EHR(electronic health records)系统中生成的,因此可能包含系统性偏差。这是一个有趣的研究方向,以探索在这些基准上训练的模型如何推广到其他临床数据集。
方法
我们用样本一词来指代由机器学习模型处理的单个记录。通常情况下,每一个预测都有一个样本。
- 对于像表型学这样的任务,样本包括整个 ICU 病程。
- 对于需要按小时进行预测的任务(例如LOS),样本包括所有在某一时间点之前发生的事件,因此一个单独的 ICU 病程会产生多个样本。
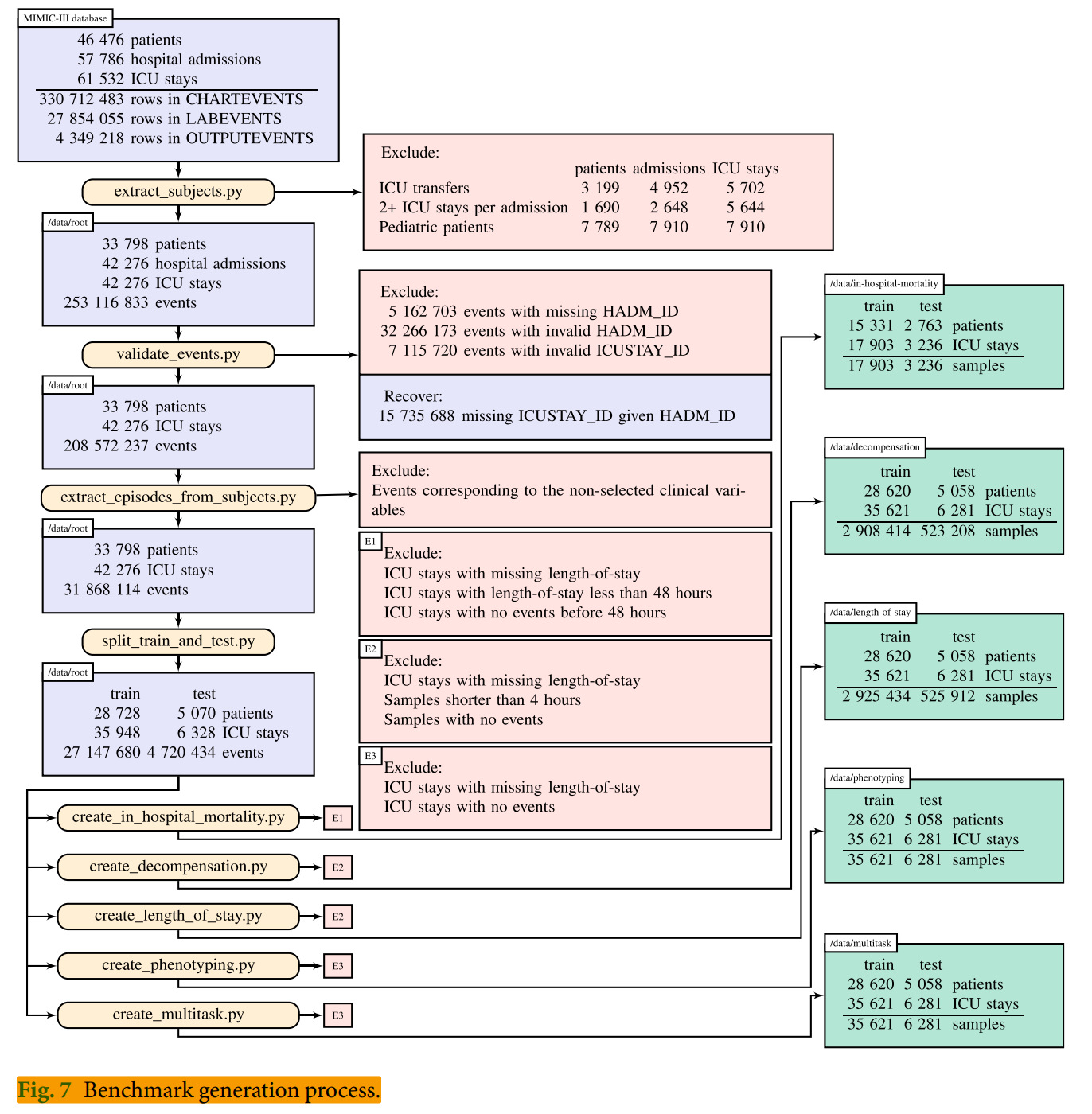
基准准备工作流程,如下图所示:
在 extract_subjects.py中,我们从原始 MIMIC-III 表中提取相关数据,并按病人整理。
- 排除任何有多次 ICU 留观或因病情需要在不同 ICU 或病房之间转诊的医院入院记录。这减少了与医院留观而非 ICU 留观相关的结局不确定性。
- 由于成人和儿科生理学之间的显著差异,我们排除了所有 ICU 留观小于 18 岁的患者。
validate_events.py 过滤掉 4500 万个无法可靠地与我们的队列中的 ICU 留住匹配的事件。
- 它会删除所有没有入院ID(HADM_ID)的事件。
- 排除那些在数据库stays.csv中没有入院ID的事件,该数据库连接了ICU停留属性(例如停留时间和死亡率)到入院ID。
- 它考虑缺失的 ICU 停留 ID(ICUSTAY_ID)。对于所有此类事件,ICUSTAY_ID 可靠地通过查看 HADM_ID 恢复。
- 脚本排除了所有未在数据库stays.csv 中列出的ICUSTAY_ID 的事件。
extract_episodes_from_subjects.py,为每个样本序列构建时间事件序列,仅保留预定义列表中的变量,并进行进一步清理。
split_train_and_test.py中,我们固定了测试数据集,包括 15% (5,070 份) 的患者、6,328 次 ICU 留观 和 470 万条事件。
模型
逻辑回归
对于每个变量,我们在给定时间序列的七个不同子序列上计算六个不同的样本统计特征。
这七个子序列包括整个时间序列、前 10% 的时间、前 25% 的时间、前 50% 的时间、后 50% 的时间、后 25% 的时间和最后 10% 的时间。
每个子序列的六个特征包括最小值、最大值、均值、标准差、偏度和测量次数。
当一个子序列不包含任何测量时,该子序列对应的特征被标记为缺失。
总体而言,我们为每个时间序列获得了 17×7×6=714 个特征。缺失值通过训练集上的平均值来代替。
然后,通过对减去均值并除以标准偏差来进行标准化。
我们针对死亡、衰竭和 25 种表型中的每一种训练了一个单独的逻辑回归分类器。
就入住天数而言,我们训练了一个softmax 回归模型来解决分桶后的十类问题。
标准LSTM
复习一下LSTM基础:链接
LSTM 是一种旨在捕获序列数据中长期依赖关系的递归神经网络。它以长度为 T 的序列 ${x_t}^T_{t\geq1}$ 作为输入,并通过以下方程输出一个长度为 T 的隐藏状态向量 ${h_t}^T_{t\geq1}$
我们将 $h_t=LSTM(x_t,h_{t−1})$ 简化为上面的方程。我们在 LSTM 层之间非循环连接和输出之前应用了 dropout。
- 对于基于LSTM的模型,我们对时间序列进行重采样以获得均匀间隔。如果同一区间内有多个变量值,则使用最后一个测量值。
- 对于缺失值,我们会用最近的测量值来填充(如果存在的话);否则,我们会用一个预先指定的“正常”值。
- 此外,我们还为每个变量提供了一个二进制掩码输入,用于指示包含真实(而非插补)测量的时间步长。
- 对于分类变量(甚至是二元变量),我们使用独热编码进行编码。数值输入通过减去均值并除以标准差来进行标准化。在填充缺失值后,每种变量都计算其统计信息。
在离散化和标准化步骤后,我们为每个 ICU 留住获得了 17 对时间序列:$({\mu_t^{(i)}}^T_{t\geq1},{c_t^{(i)}}^T_{t\geq1})$
- 其中,$\mu_t^{(i)}$是一个二进制变量,表示变量 i 是否在时间步长 t 被观察到。
- $c_t^{(i)}$是变量 i 在时间步长 t 的值(即被观察到或插补过的)。
通过 ${x_t}^T_{t\geq1}$ 表示所有 ${\mu_t^{(i)}}^T_{t\geq1} $和 ${c_t^{(i)}}^T_{t\geq1}$ 时间序列的串联,其中串联是在变量轴上进行的。$x_i$ 成为了长度为76的向量。
我们还为每次住院制定了一组目标:
- ${d_t}^T_{t\geq1}$,$d_t \in {0,1}$,是代偿失调的 T 个二进制标签列表,每个小时一个。
- $m\in{0,1}$,是单个二进制标签,表示患者是否在医院死亡。
- ${\ell_t}^T_{t\geq1}$,$\ell_t \in \mathbb{R}$,是每个时间步剩余停留时间(出院前剩余时间)的实数值列表。
- $p_{1:K} \in {0,1}^K$是一个大小为 K 的二进制表型标签向量。
当在每个时间点,训练我们的模型以预测剩余住院长度时,我们会使用一组分类标签${l_t}^T_{t\geq1}$,$l \in {1,2…..10}$,表示属于十个中的哪个桶$\ell_t$。当在方程式中使用它们(例如作为softmax输出或损失函数的一部分),我们将$l_t$解释为一个“十进制热编码”的二进制向量,第 i 个是$l_{ti}$。
请注意,由于在基准任务的创建过程中应用了特定于任务的过滤器,因此我们可能会遇到给定停留时间 m 丢失或/和某些时间步长的 $d_t$、$\ell_t$ 丢失的情况。在不滥用我们的方程符号的情况下,我们将假设所有目标都存在。在代码中,丢失的目标将被丢弃。
我们描述了每个基准任务实例的符号:
- 每例入住医院后死亡预测任务的实例都是一个二元组$({x_t}^{48}_{t\geq1},m)$,其中x 是前 48 小时 ICU 留观的临床观察矩阵,m 是标签。
- 衰竭和住院时间预测任务的实例是一个二元组$({x_t}^{\tau}_{t\geq1},y)$,其中x 是前 $\tau$ 小时留观的临床观察矩阵,y 是目标变量。
- 每例表型分类任务的实例都是一个二元组$({x_t}^T_{t\geq1},p_{1:K})$,其中x 是整个 ICU 留观期间的观察矩阵,$p_{1:K} $是表型标签。
我们的第一个基于LSTM 的基线方法采用一个预测任务的示例$({x_t}^{T}{t\geq1},y)$,用单个 LSTM 层处理输入:$h_t=LSTM(x_t,h{t−1})$。为了预测目标,我们在其上添加输出层,同时给出损失函数:
其中,$CE(y,\hat{y})$ 是二元交叉熵,而 $MCE(y,\hat{y})$ 是定义在 C 个类上的多类交叉熵: \(CE(y,\hat{y})=-(y\cdot log(\hat{y})+(1-y)\cdot log(1-\hat{y}))\)
\[MCE(y,\hat{y})=-\sum^C_{k=1} y_klog(\hat{y}_k)\]我们称这种模型为“标准LSTM”。
Channel-wise LSTM
虽然标准 LSTM 网络直接在时间序列 ${x_t}^{T}{t\geq1}$ 的连接上工作,但 Channel-wise LSTM 使用双向 LSTM 层对每个变量的独立数据$({\mu_t^{(i)}}^T{t\geq1},{c_t^{(i)}}^T_{t\geq1})进$行预处理。
对于不同的变量,我们使用不同的 LSTM 层。然后将这些 LSTM 层的输出连接起来,并馈送给另一个 LSTM 层。
$\overleftarrow{x_t}$代表序列 ${x_t}^{T}_{t\geq1}$ 的反转中的第 t 个元素。每个任务的输出层和损失函数与标准 LSTM 基线相同。
使用 Channel-wise 模块背后的原因有两个:
- 它有助于在与其他变量的数据混合之前对单个变量的数据进行预处理。这样模型可以学习存储只与特定变量有关的一些有用信息。例如,它可以学习存储早期时间步骤的最大心率或平均血压。这种信息很难通过标准LSTM来学习,因为输入到隐藏权重矩阵需要稀疏行。
- 这种通道模块通过明确显示掩码变量与哪些变量相关来促进缺失数据信息的纳入。这些信息可能难以通过标准LSTM模型学习。
注意,这个按通道的模块可以替代任何神经架构中的输入层,该神经架构以不同变量的时间序列的串联作为其输入。
深度监督
到目前为止,我们已经定义了在最后一步进行预测的模型。这样,监督就来自最后的时间步,这意味着模型需要跨多个时间步传递信息。我们提出了两种方法,在每个时间步骤对模型进行监督。我们用“深度监督”来指代它们。
在医院死亡率和表型预测任务中,我们使用目标复制来实现深度监督。 在这种方法中,我们在所有时间步长上复制目标,并通过更改损失函数要求模型也预测复制的目标变量。 这些深度监督模型的损失函数如下:
- $\alpha \in [0,1]$,是一个超参数,用于表示目标复制部分在损失函数中的强度。
- $\hat{d}_t$ 表示时间步长 t 的代偿失调预测。
- $\hat{p}_{tk}$表示时间步长 t 时第 k 种表型的预测。
对于代偿失调和停留时间预测任务,我们不能使用目标复制,因为最后一个时间步的目标对其他时间步是错误的。由于在这些任务中,我们可以从单个ICU停留期间创建多个预测实例,因此可以分组这些样本并一次通过进行预测。这样,每个时间步都有一个目标,并且模型将在每个时间步上进行监督。这些深度监督模型的损失函数如下:
请注意,每当我们将单个 ICU 留院观察的时间段分组时,我们会使用简单的从左到右的 LSTM 而不是双向 LSTM,以便不使用来自未来时间步的数据。
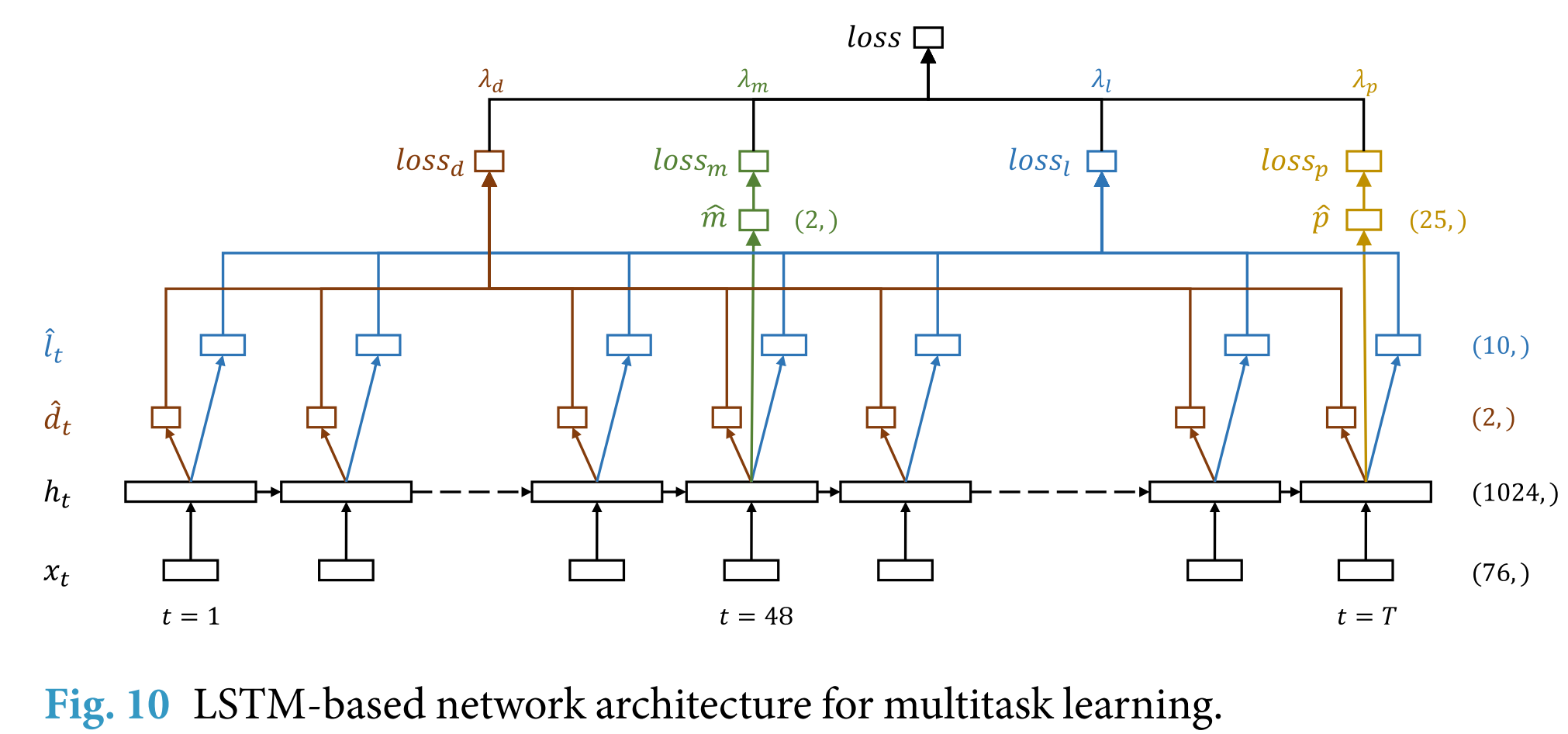
多任务学习 LSTM
对于每个任务,我们提出另一个基线,其中我们尝试使用其他三个任务作为辅助任务来提高性能。可以使用标准LSTM或通道级LSTM来实现这种多任务处理。
在多任务设置中,我们将来自单个 ICU 住院的示例分组,并联合预测与单个 ICU 相关的所有目标。这意味着我们使用代偿失调和停留时间预测任务的深度监督。我们可以选择是否要使用深度监督来执行院内死亡率和表型预测任务。
- 对于院内死亡率,我们只考虑前48个时间步长${x_t}^{t_m}{t\geq1}$,通过添加一个带sigmoid激活函数的密集层来预测 $t_m=48$ 的 $\hat{m}$。该层使用$h{t_m}$作为输入。
- 对于代偿失调,我们采用全部 ${x_t}^{T}{t\geq1}$,并且在每个时间步骤上通过添加一个 dense 层来产生死亡预测序列 ${\hat{d}}^{T}{t\geq1}$
- 对于表型,我们考虑完整的序列,但在最后的时间步长 T,通过添加25个并行的具有 Sigmoid 激活函数的密集层来预测表型 $\hat{p}$
- 我们在每个时间步长上通过添加单个密集层来预测LOS。
每个任务的损失函数与深度监督设置中的相同。总体损失是特定于任务的损失的加权总和:
\[\mathcal{L}_{mt}=\lambda_d \cdot \mathcal{L}_d^* + \lambda_l \cdot \mathcal{L}_l^* + \lambda_m \cdot \mathcal{L}_m^* + \lambda_p \cdot \mathcal{L}_p^*\]其中权重是非负数。对于原始的住院时长预测,我们在多任务损失函数中用 $\mathcal{L}l^*$ 代替 $\mathcal{L}\ell^*$
实验、模型选择与评估
对于所有算法,我们使用预定义训练集中预先设定的 15% 的患者的数据作为验证数据,并在剩余的 85% 上训练模型。我们根据验证集性能使用网格搜索来调整所有超参数。每个基线的最佳模型都是根据验证集上的性能表现来选择的。最终分数是在测试集上报告的,在模型开发过程中,我们很少使用测试集,以避免无意中泄露测试集。
逻辑回归
逻辑回归模型唯一的超参数是L1和L2正则化系数。在我们的实验中,L1和L2惩罚是互斥的,并且不应用于偏差项。我们使用网格搜索来找到最佳惩罚类型及其正则化系数。
- 在代偿失调预测中,表现最好的逻辑回归使用了L2正则化,C = 0.001。
- 在表型预测中,表现最好的逻辑回归使用了L1正则化,C = 0.1。
- 在住院时间预测中,表现最好的逻辑回归使用了L2正则化,C = $10^{-5}$。
LSTM
在对基于LSTM的模型进行离散化时,我们设置等间隔间隔的长度为1小时。这在缺失数据的数量和落入同一区间相同变量的数量之间取得了合理的平衡。这一选择也与衰竭和LOS预测任务中采样预测示例的速度一致。我们也尝试了0.8小时长度的间隔,但结果没有改善。
对于基于LSTM的模型,超参数包括:
- LSTM层中的记忆单元数量
- 丢弃率
- 是否使用一个或两个LSTM层。
Channel-wise LSTM模型有一个额外的超参数:
- 通道内LSTM中的单元数(所有17个LSTM具有相同的单元数)。
深度监督中的超参数:
- 每当目标复制被启用时,我们在相应的损失函数中将α设置为0.5。
LSTM 模型的最佳超参数取值因任务而异。它们在我们的代码存储库中的 pre_trained_models.md 文件中列出。一般来说,我们注意到 dropout 在减少过拟合方面有很大帮助。事实上,在医院内死亡率预测(其中过拟合问题最严重)这一基准任务中,所有基于 LSTM 的基线模型都使用了 30% 的 dropout。
所有基于 LSTM 的模型都是使用 Adam 优化器 和 10−3 的学习率以及β=0.9 训练的。批大小设置为 8、16 或 32,具体取决于计算单元可用的内存量。我们没有对调整优化器超参数和批量大小以提高性能进行大量实验。
多任务
对于多任务模型,我们有四个超参数:损失函数中的 $λ_d, λ_m,λ_l, λ_p$ 权重。我们没有对这些超参数进行完整的网格搜索。相反,我们尝试了五个不同的 λ 值$(λ_d, λ_m,λ_l, λ_p)$ :
- (1, 1, 1, 1);
- (4, 2.5, 0.3, 1);
- (1, 0.4, 3, 1)
- (1, 0.2, 1.5, 1)
- (0.1, 0.1, 0.5, 1)
第一个具有每个任务相同的权重,而第二个试图使损失函数的四项近似相等。剩下的三个组合是通过查看每个任务的学习速度来选择的。
在多任务设置中,过拟合是一个严重的问题,其中死亡率和衰竭预测验证性能下降得比其他情况更快。所有最佳的多任务基线都使用了要么 (1, 0.2, 1.5, 1)或者 (0.1, 0.1, 0.5, 1)作为 $(λ_d, λ_m,λ_l, λ_p)$ 。第一个配置对于院内死亡率、衰竭和停留时间的预测任务表现最好,而第二个配置对于表型预测任务更好。对于表型预测任务的最佳多任务基线的 $λ_d, λ_m,λ_l $ 的值相对较小的事实支持了额外的多任务处理会损害性能的假设。
评估
最后,我们在每个基准测试集上评估最佳基线。由于测试分数是对模型在未见过的数据上的性能估计,我们使用自助法来估计分数的置信区间。自助法已被用于估计评价指标的标准差,计算不同模型之间的统计学显著差异,并报告模型的 95% 自助置信区间。提供置信区间也有助于解决所有公共基准数据集都存在的一个已知问题——对测试集的过拟合。
为了估计 95% 的置信区间,我们从测试集中随机有放回地抽取 K 次;在这些抽样集合上计算分数;并使用这些分数的第 2.5 和 97.5 百分位数作为我们的置信区间估计。对于医院内死亡率和表型预测,K=10000,而对于衰竭和停留时间预测,K=1000,因为这些任务的测试集要大得多。