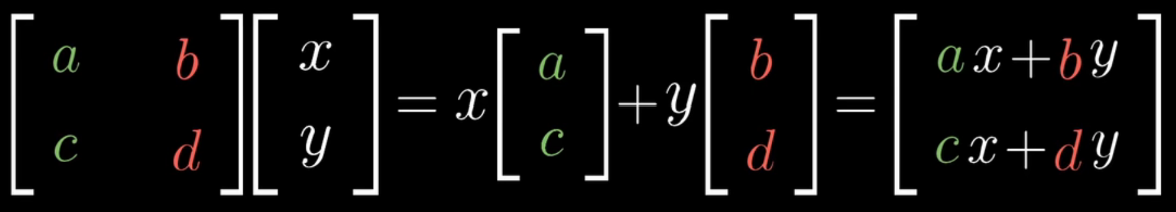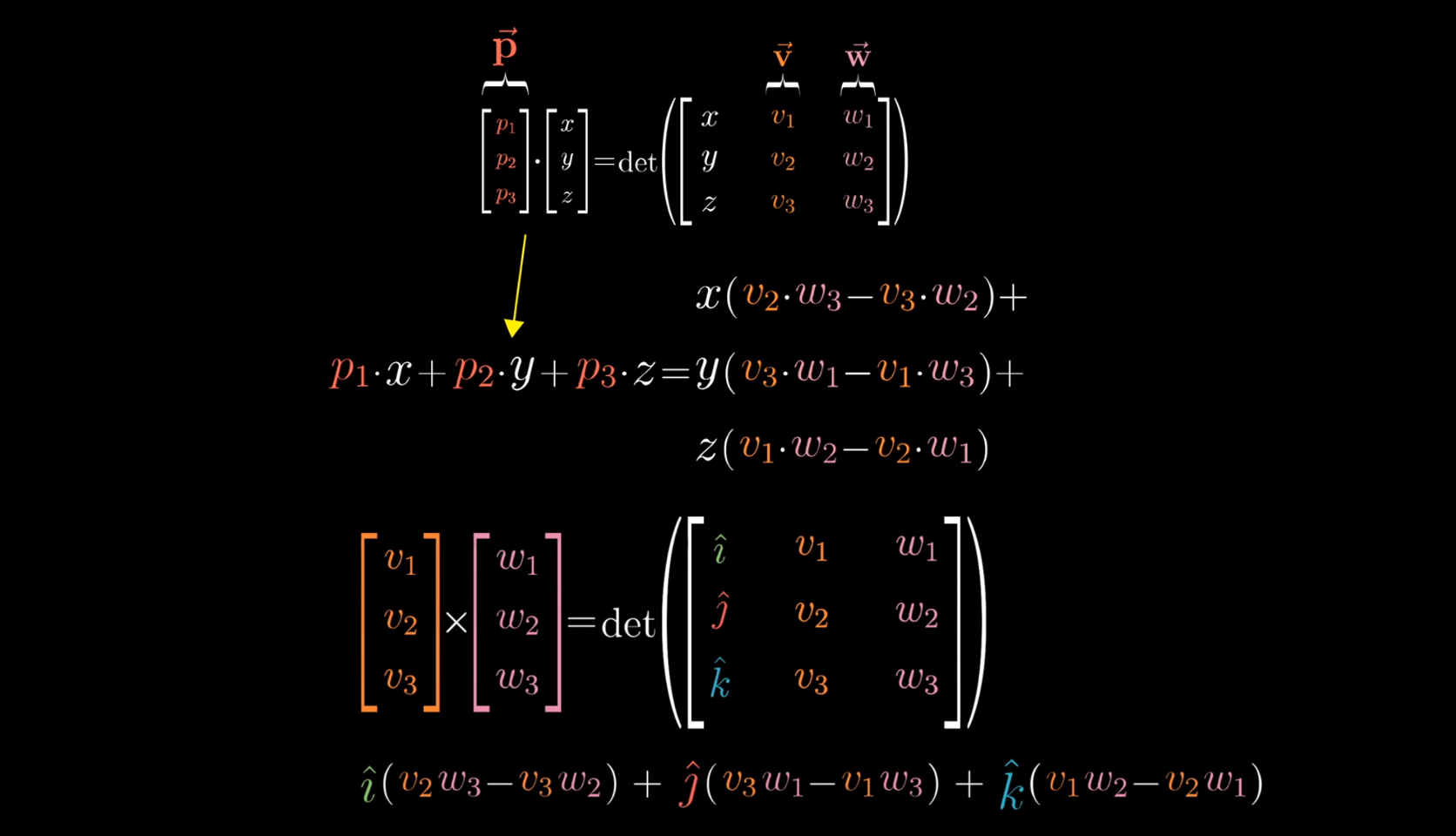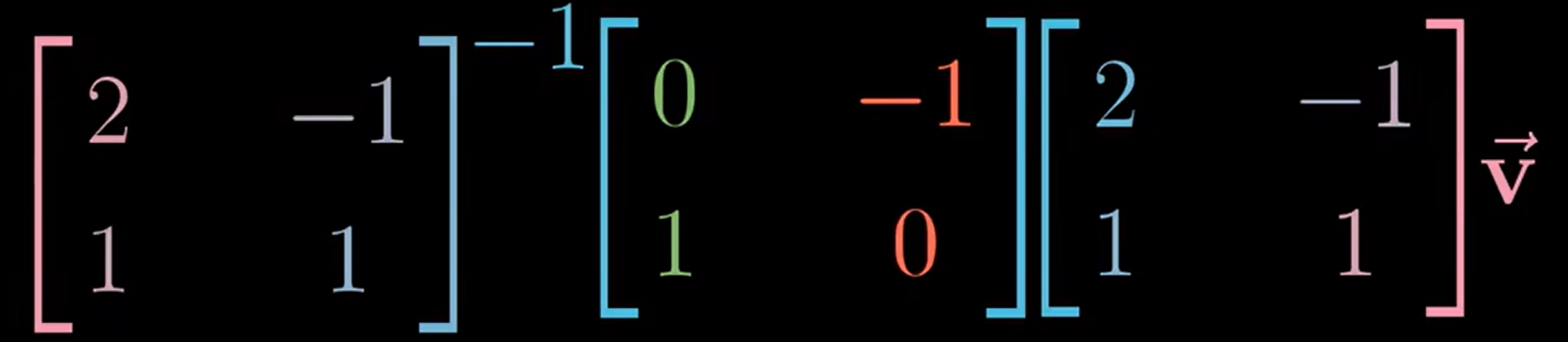线性代数的本质
向量
三种看待向量的观点
| 不同的人 | 不同的观点 |
|---|---|
| 物理专业的学生 | 空间中的箭头(长度和方向) |
| 计算机专业的学生 | 有序的数字列表 |
| 数学家 | 任何东西(以上两个观点的碰撞) |
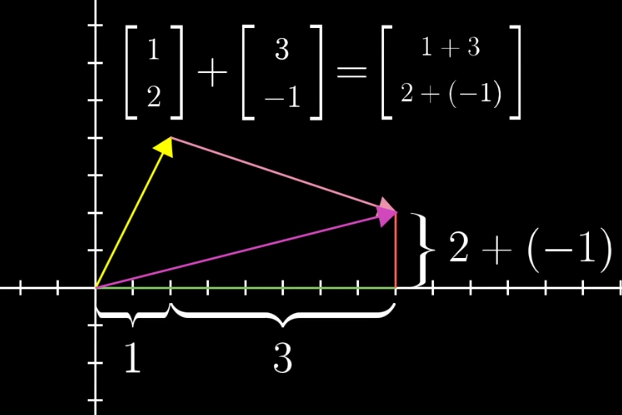
向量加法的几何意义:遵循三角形法则。如果将每个向量看作一种特定的运动,即向空间中某个方向迈出一定距离。若先沿着第一个向量方向移动,再沿着第二个向量方向移动,总体效果与沿着这两个向量和运动无异。
向量乘法的几何意义:乘以大于1的数值,就是将这个向量拉伸;乘以小于1的数值,就是将这个向量压缩;乘以负数,就是将这个向量翻转。拉伸,压缩,翻转向量的行为,统称为缩放(scaling),而这些数值本身,称之为标量(scalars)。
基
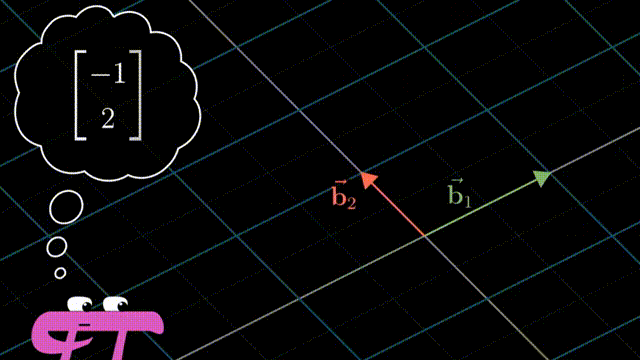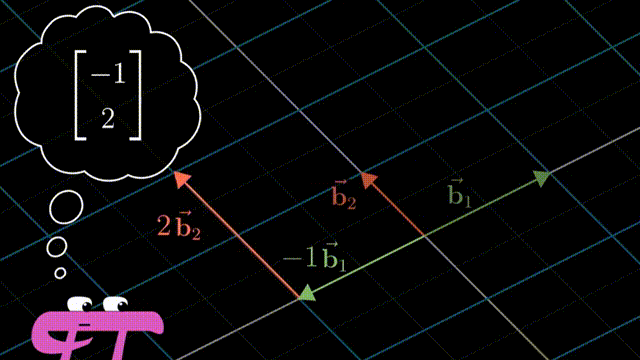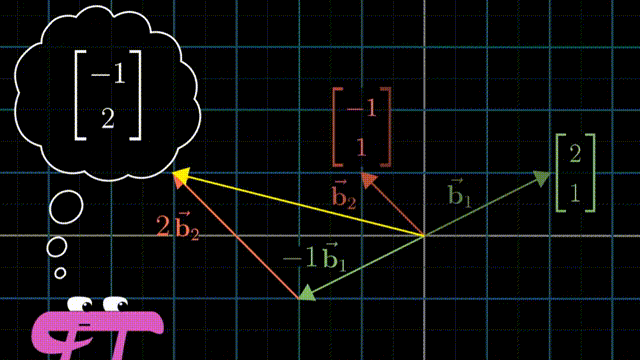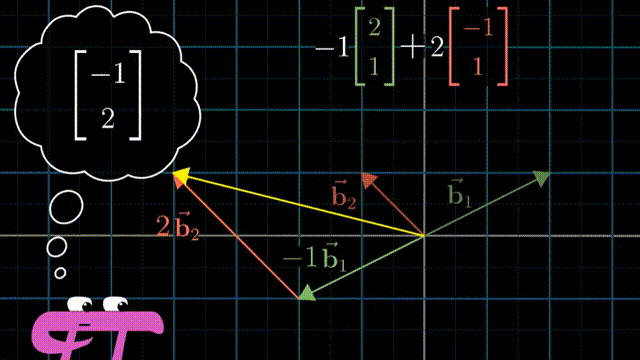
i 和 j 是 xy 坐标系中的基向量(basis vectors);其实也可以选择不同的basis vectors,比如说在平面上任意的两个向量作为基,这样得到的标量的数值是不相同的,但是同样可以通过对这一对任意选择的基向量进行线性组合(linear combination),而得到在平面上的任意向量。
基的严格定义:向量空间的一组基是张成该空间的一个线性无关的向量集。
n个线性无关(非0)向量线性组合,可以组成一个n维空间
矩阵向量乘法
线性变换从几何想象看,是一种操纵空间的手段,特点包括:
- 所有的直线还是直线
- 原点还在原来的位置
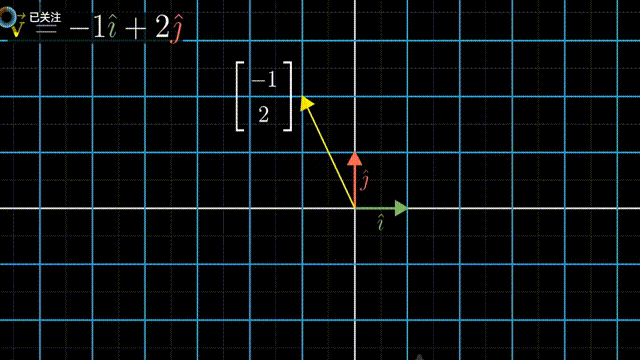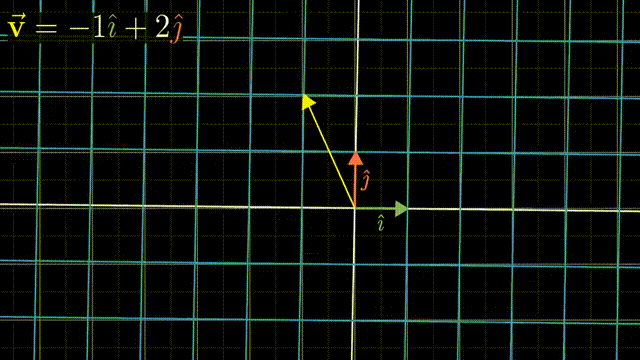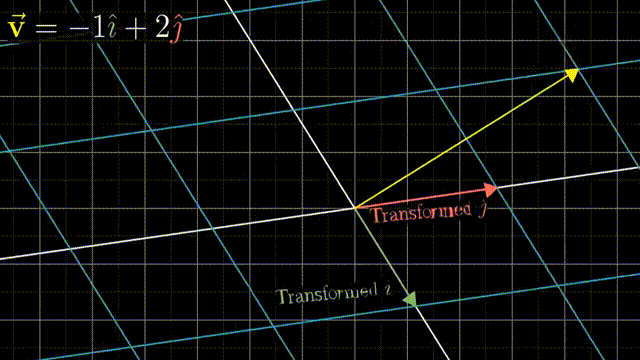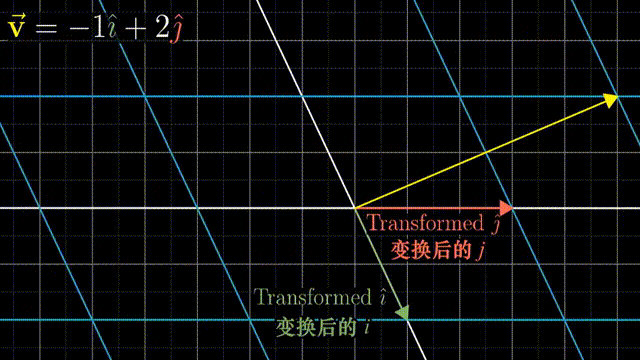
可以借助基向量的变换,可以理解整个空间的线性变换:
事实上,一个二维线性变换仅由四个数字完全确定,即基向量的变换。借助基向量的变换,我们可以得到任意一个向量$(x,y)$在线性变换后的结果。
把它抽象化之后,则得到了矩阵乘法的运算公式,并且还可见其几何意义,$(a,c)$和$(b,d)$是新空间的基
一个特殊例子,假如变换之后的向量是线性相关的,那么所有原来平面上的点在变换之后就被压缩到了一条直线上。
矩阵乘法
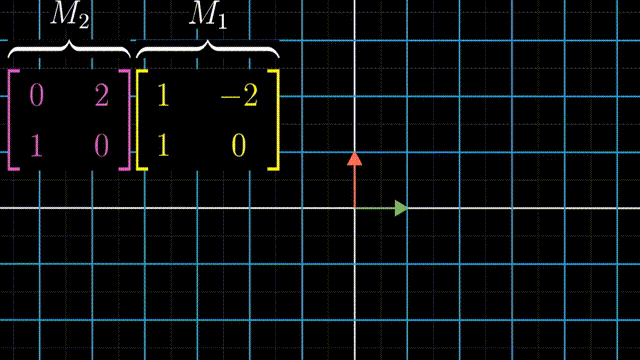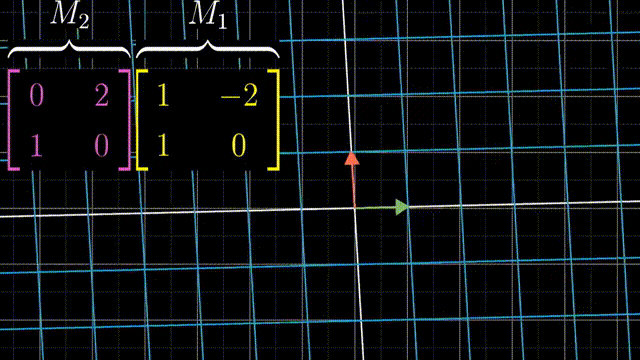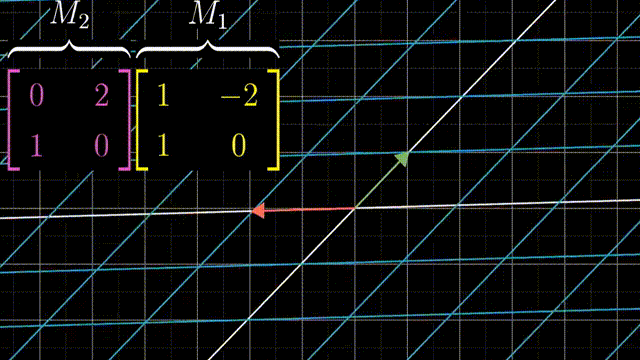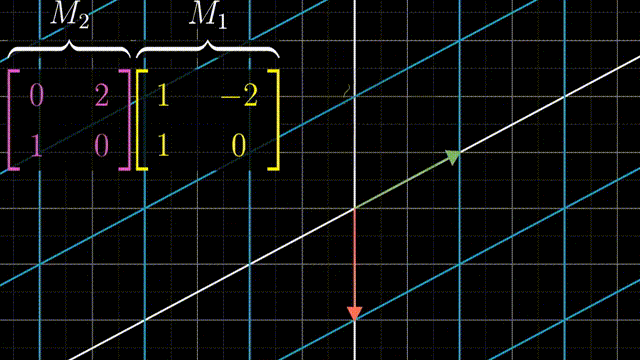
两个矩阵相乘有着几何意义,也就是两个线性变换相继作用,如图,注意先作用M1,然后M2
可以跟踪基的变化来得到矩阵乘法的结果:
行列式
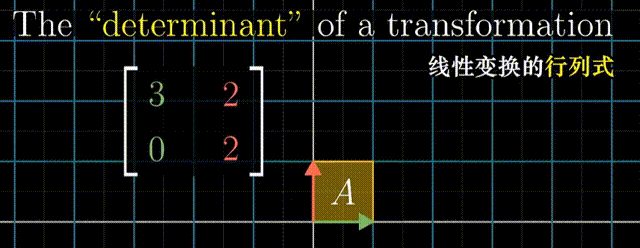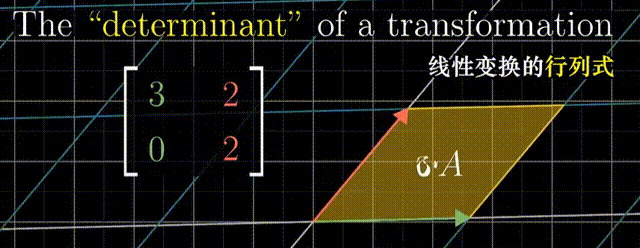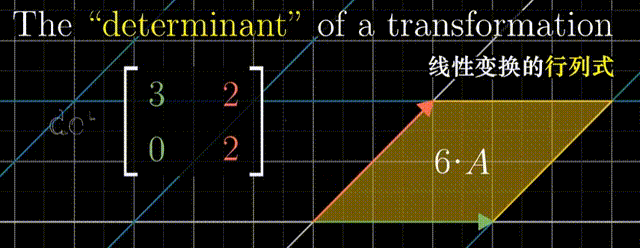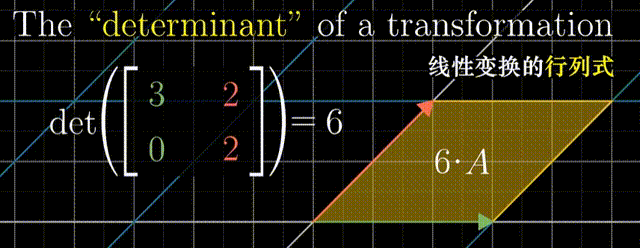
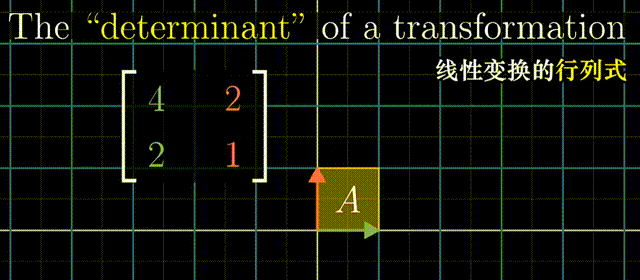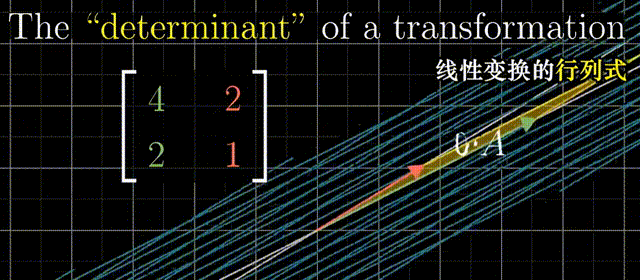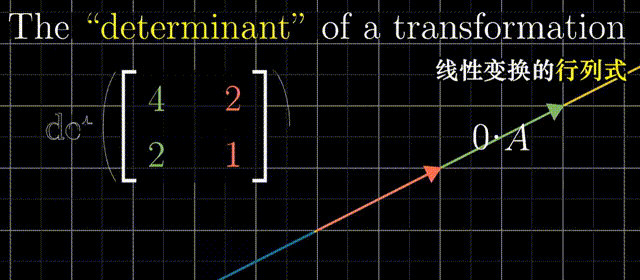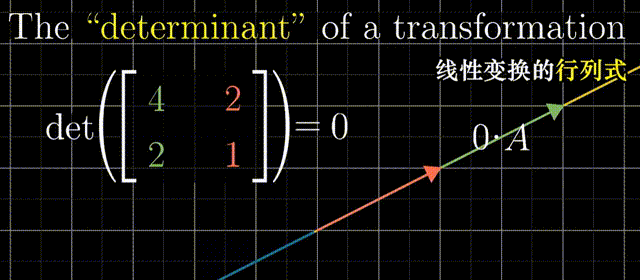
行列式:线性变换改变面积的比例。二阶行列式可看做平行四边形的面积
行列式为0,矩阵必然线性相关,或者说面积被挤压到0
行列式的正负与平面的取向有关,行列式为负,空间被翻转
三阶行列式可简单看做平行六面体的体积,正负号代表三维翻转,如果可以用右手系表示为正,如果只能用左手系表示为负
严谨的面积计算方法:
线性方程组
线性方程组与向量方程的转换:
\[\left\{ \begin{array}{l} 2x + 5y +3z = -3 \\ 4x + 0y +8z = 0 \\ 1x+3y+0z=2 \end{array} \right. \to \begin{bmatrix} 2 & 5 & 3 \\ 4 & 0 & 8 \\ 1 & 3 & 0 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} =\begin{bmatrix} -3 \\ 0 \\ 2 \\ \end{bmatrix}\]可以视作$A\vec{x}=\vec{v}$,可以这么理解:我们要找到一个未知的 $\vec{x}$,让它经历空间变换后变成 $\vec{v}$
如果$det(A)\neq 0$,我们可以找到它的逆矩阵 $A^{-1}$,相当于把转换好的空间转换回去。在方程两边同乘。
为什么行列式不能等于0?回忆一下,行列式等于0相当于把一个高维空间挤压成一个低维空间,它的逆矩阵相当于要把低维空间转换为高维空间。这是做不到的。它脱离了函数的概念,即一个x对应一个y,在低维空间转换为高维空间的过程中,低维空间的一个点要转换为高维空间的线、面等等,相当于一个x对应多个y
行列式等于0时,可能有解,仅当 $\vec{v}$ 恰好在挤压成的低维空间上。
秩
秩代表着变换后空间的维数。
举个例子,当变换的结果为一条直线时(一维),我们称这个变换的秩为1。
比如说对于2×2的矩阵,它的秩最大为2,意味着基向量仍旧能张成整个二维空间,并且矩阵的行列式不为零。但是对于3×3的矩阵,秩为2意味着空间被压缩了。
零空间
对于一个非满秩的矩阵来说,它将空间压缩到一个更低的维度上,也就是说会有一系列向量在变换后成为零向量(直线降维为点)。
举些例子:如果一个二维线性变换将空间压缩到一条直线上(降维),那么沿不同方向直线上的所有向量就被压缩到原点。
如果 一个三维线性变换将空间压缩到一条直线上,那么就有一整个平面上的向量在变换后落在原点。
变换后落在原点的向量的集合,被称为矩阵的零空间或核。变换后一些向量落在零向量上,而“零空间”正是这些向量所构成的空间。
对线性方程组$A\vec{x}=\vec{0}$,矩阵A的零空间就是方程的解。
非方阵
非方阵体现了不同维数之间的变换。
如果2×2矩阵表示二维向量到二维向量的变换,3×3矩阵来表示的三维向量到三维向量的变换,那么自然的,3×2矩阵肯定是二维向量与三维向量的转换,但是从谁转换到谁呢?
对于3×2矩阵,矩阵有两列表明输入空间有两个基向量,有三行表明每一个基向量再变换后都用三个独立的坐标来描述,因此几何意义是将二维空间映射到三维空间上。
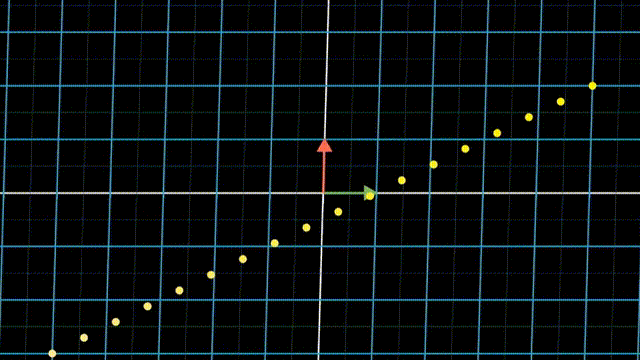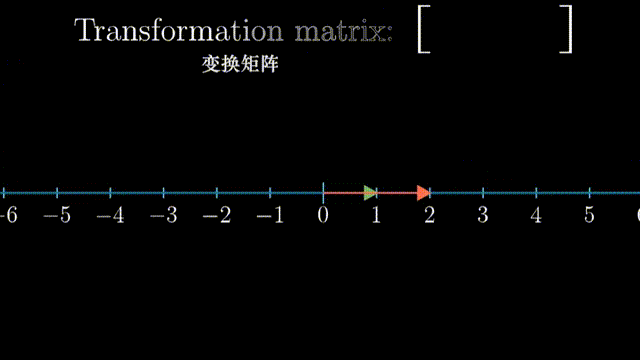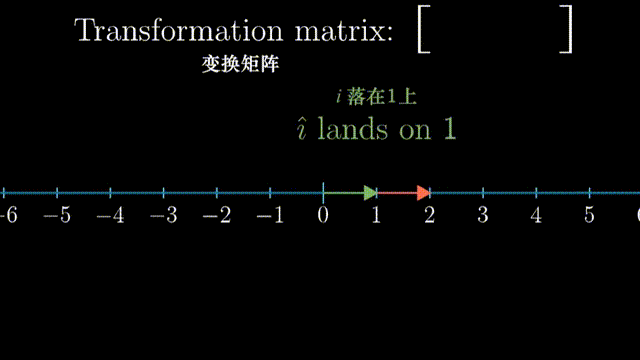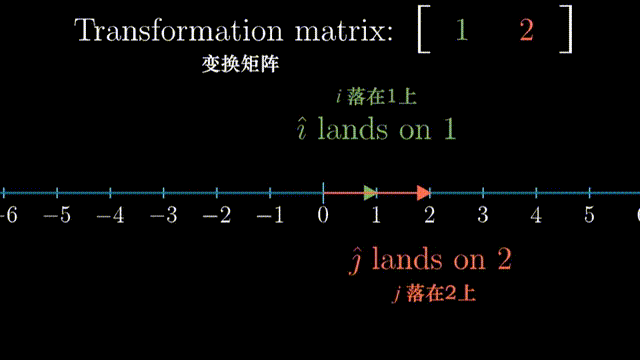
我们举一个动画例子,1×2的矩阵代表将二维空间映射到一维空间上:
向量点积
\[\begin{bmatrix} 2 \\ 4 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \\ \end{bmatrix} = 2\times1+4\times2=10\] \[\begin{bmatrix} 2 & 4 \\ \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ \end{bmatrix} = 2\times1+4\times2=10\]向量点积和矩阵乘十分相似!这不是巧合。 在矩阵乘的例子中,1×2的矩阵代表将二维空间映射到一维空间上,一个向量接受这个转换,成为了数。
实际上,我们现在可以说,1×2矩阵与二维向量之间有着微妙的联系。这种关系在于:将向量放倒,从而得到与之相关的矩阵,或者将矩阵直立,从而得到与之相关的向量。
向量叉乘
对于二维向量的叉乘,即求其行列式,结果是一个数。复习一下,二阶行列式可看做平行四边形的面积,行列式的正负与平面的取向有关。
\[\vec{u}\times \vec{w}=\begin{bmatrix} 2 \\ 4 \\ \end{bmatrix} \times \begin{bmatrix} 1 \\ 2 \\ \end{bmatrix} = \det \left( \begin{bmatrix} 2&1 \\ 4&2 \\ \end{bmatrix} \right)\]我们自然而然地想要推广到三维情况:
\[\vec{u}\times \vec{v}\times\vec{w}= \det \left( \begin{bmatrix} u_1 & v_1 & w_1 \\ u_2 & v_2 & w_2 \\ u_3 & v_3 & w_3 \\ \end{bmatrix} \right)\]但事实上这是错的!如果你之前学过线性代数,就知道两个三维向量的叉乘是另外一个三维向量,长度为两个向量围成的平行四边形的面积,方向与原先两个向量垂直(复习一下右手定则)如果用公式表示:
\[\vec{v}\times\vec{w}= \det \left( \begin{bmatrix} i & v_1 & w_1 \\ j & v_2 & w_2 \\ k & v_3 & w_3 \\ \end{bmatrix} \right)\]给出的公式与教材上不同,但是因为转置不影响行列式的值,所以没关系,这么写方便直观理解
为了直观理解,我们创建一个三维到一维的函数,假设 $\vec{v}$ 和 $\vec{w}$ 是固定的,这个函数的几何意义是,对于任一输入的向量 ,输出由它和 $\vec{v}$ 和 $\vec{w}$ 确定的平行六面体体积(有正负):
\[f\left( \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} \right) = \det \left( \begin{bmatrix} x & v_1 & w_1 \\ y & v_1 & w_1 \\ z & v_1 & w_1 \\ \end{bmatrix} \right)\]这个函数是线性的,那么同样,三维到一维可以用空间转换,即1×3矩阵的来表示:
\[f\left( \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} \right) = \begin{bmatrix} p_1 &p_2&p_3 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix}\]当我们把 $\vec{p}$ 立起来之后,我们可以发现它与叉乘公式的对应:
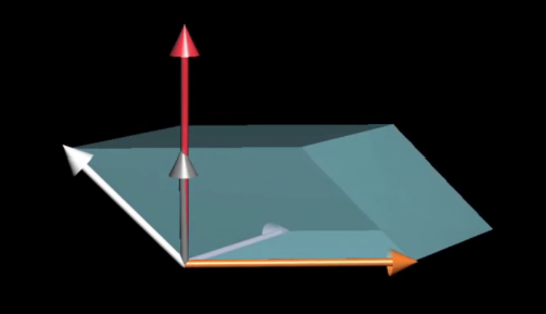
先看上面的式子,当你将向量p和某个向量(x,y,z)点乘时,所得结果等于一个由(x,y,z)和v与w确定的平行六面体的有向体积,什么样的向量p才能满足这一特殊性质?答案是垂直于v和w且长度为平行四边形面积的向量。
证明过程:
\[平行六面体的有向体积 = u,w平行四边形的面积 \times (x,y,z)垂直于平行四边形方向上的分量\] \[平行六面体的有向体积 = (x,y,z) 点乘 垂直于v和w且长度为平行四边形面积的向量\]如果我们令平行四边形的面积为S,(x,y,z)长度为 a,(x,y,z) 与垂线的夹角为 $\theta$,上面两个等式都可以证明为:
\[V=Sa \sin(\theta)\]得出结论:在叉乘公式中插入i、j和k不过是在传递一个信号,告诉我们应该把这些系数解读为一个向量的坐标。p就是v与w的叉乘。叉乘的目标是找到p,使得任意个向量(x,y,z)与p点乘(或者说三维到一维的转换)后等于平行六面体的有向体积。
相似变换
教科书:如果 $P^{-1}AP=B$,那么 A 与 B 相似,P称为相似变换矩阵
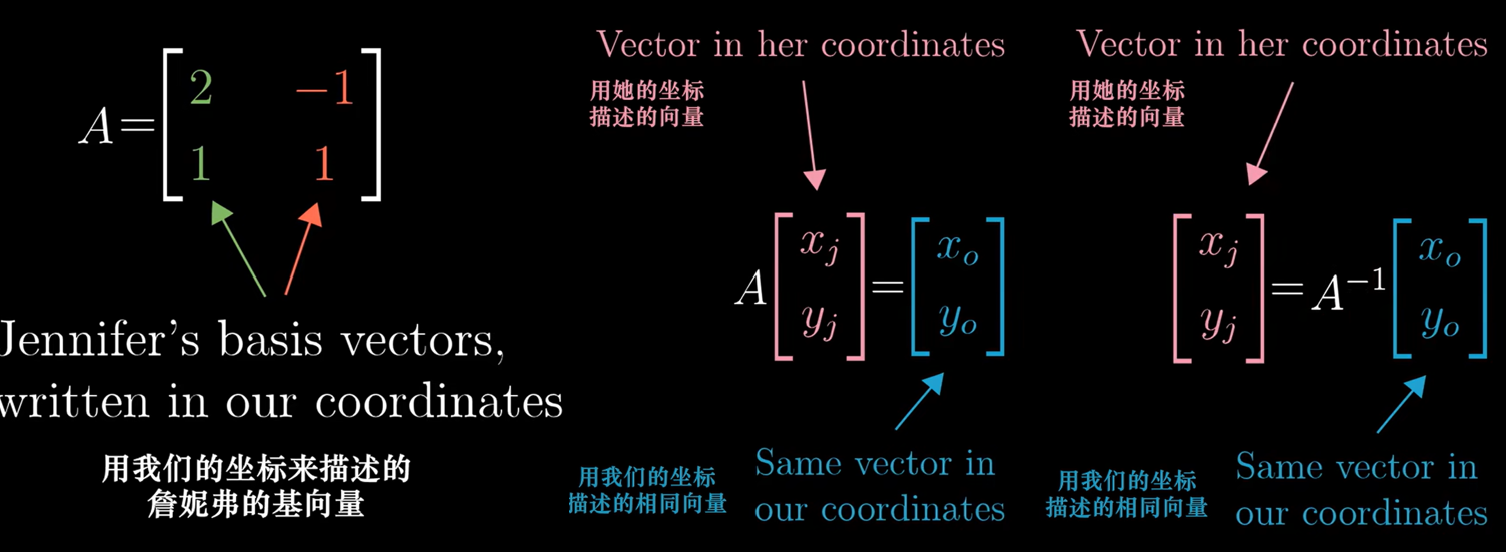
我们从直观的角度理解什么是 $P^{-1}AP$,让我们讲一个故事:当我使用基向量(0,1)和(1,0),Jenny使用基向量 (2,1)和(-1,1) 时,可以看作我们使用不同的语言。
问题来了,Jenny用(-1,2)表示一个向量,在我的坐标系如何描述?(如何从她的语言转化到我的语言?)
\[\begin{bmatrix} 2 & -1 \\ 1 & 1 \\ \end{bmatrix} \begin{bmatrix} -1 \\ 2 \\ \end{bmatrix} = \begin{bmatrix} -4 \\ 1 \\ \end{bmatrix}\]复习一下,用Jenny的基向量组成的矩阵代表一种转换,将我的网格变换为Jenny的网格。然而从语义上,却是将她的语言转化为我的语言(相反的)
可以把它看作我们对Jenny的向量的误解(-1,2),变换成Jenny真正想表示的向量(-4,1)
当把矩阵求逆,即将Jenny的网格变换为我的网格;将我的语言转化为她的语言
继续下一个问题,在我的坐标系中的空间转换(矩阵 M),如何在Jenny的坐标系中表示?
拿一个Jenny的向量 $\vec{v}$ 举例:
- 首先乘矩阵 $A$ ,转换为我的语言。
- 然后乘矩阵 $M$,在我的坐标系中的空间转换完毕。
- 然后乘矩阵 $A^{-1}$,转换为Jenny的语言。完毕。
因此,在我的坐标系中的空间转换(矩阵 M),在Jenny的世界中用 $A^{-1}MA$ 表示
总的来说,每当看到这样一个表达式:$A^{-1}MA$,这就暗示着一种数学上的转移作用,中间的矩阵代表一种你所见的变换,而外侧两个矩阵代表着转移作用,也就是视角上的转化。矩阵乘积仍然代表着同一个变换,只不过是从其他人的角度来看的。
特征值与特征向量
考虑二维空间中的线性变换,一个向量张成的空间,是通过原点和向量尖端的直线。
大部分向量在变换中都离开了其张成的空间,不过,某些特殊向量的确留在它们张成的空间里,意味着矩阵对它的作用仅仅是拉伸或者压缩而已。而这些特殊向量是特征向量,特征值代表特征向量在变换中拉伸或压缩的比例。
这也与我们学过的公式对应:
\[A\vec{v} = \lambda \vec{v}\]考虑一个三维空间中的旋转。如果你能找到这个旋转的特征向量,也就是留在它张成的空间里的向量,那么你找到的就是旋转轴。在这种情况下,相应的特征值必为1,因为旋转并不缩放任何一个向量。
再考虑我们学过的一个定律:如果方阵 A 可被相似对角化,那么存在 $P^{-1}AP=\Lambda$ 为对角矩阵。怎么证明?
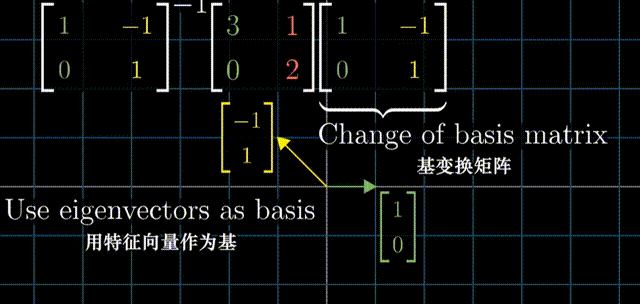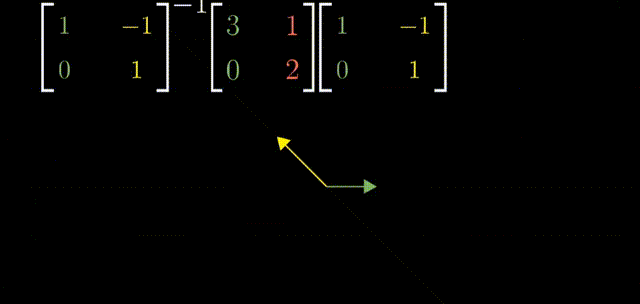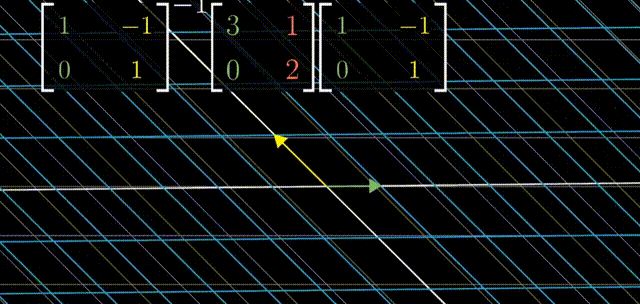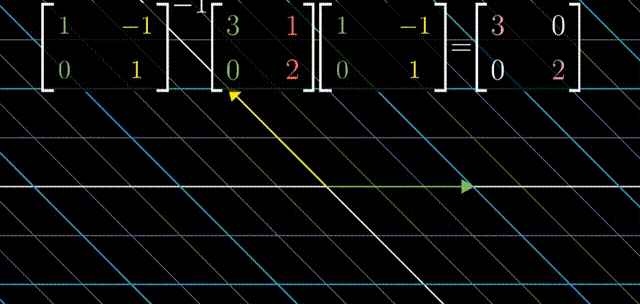
问一个问题:对于一个矩阵(空间转换),如果用特征向量作为新的基,在新的坐标系中,这个矩阵(空间转换)是怎样的?
具体来说,取出两个特征向量,将坐标作为矩阵的列,这个矩阵就是基变换矩阵。在右侧写下基变换矩阵,在左侧写下基变换矩阵的逆。当你将原始的变换夹在两个矩阵中间时,所得的矩阵代表的是同一个变换,不过是从新基向量所构成的坐标系的角度来看的。(复习一下上面的“相似变换”章节)
用特征向量来完成这件事的意义在于这个新矩阵必然是对角的,并且对角元为对应的特征值。这是因为,在新的坐标系中,基向量(同样是特征值)没有离开张成的空间,基向量在变换中只进行了缩放。
普适的代价是抽象。
但是具体的例子帮助我们学习。