Graph Attention Networks
读论文时间!
图注意力网络:GAT
参考:
介绍
图注意力网络(Graph Attention Networks, GAT),处理的是图结构数据。它通过注意力机制(Attention Mechanism)来对邻居节点做聚合操作,实现了对不同邻居权重的自适应分配,大大提高了图神经网络的表达能力。
核心观点:GAT (Graph Attention Networks) 采用 Attention 机制来学习邻居节点的权重, 通过对邻居节点的加权求和来获得节点本身的表达
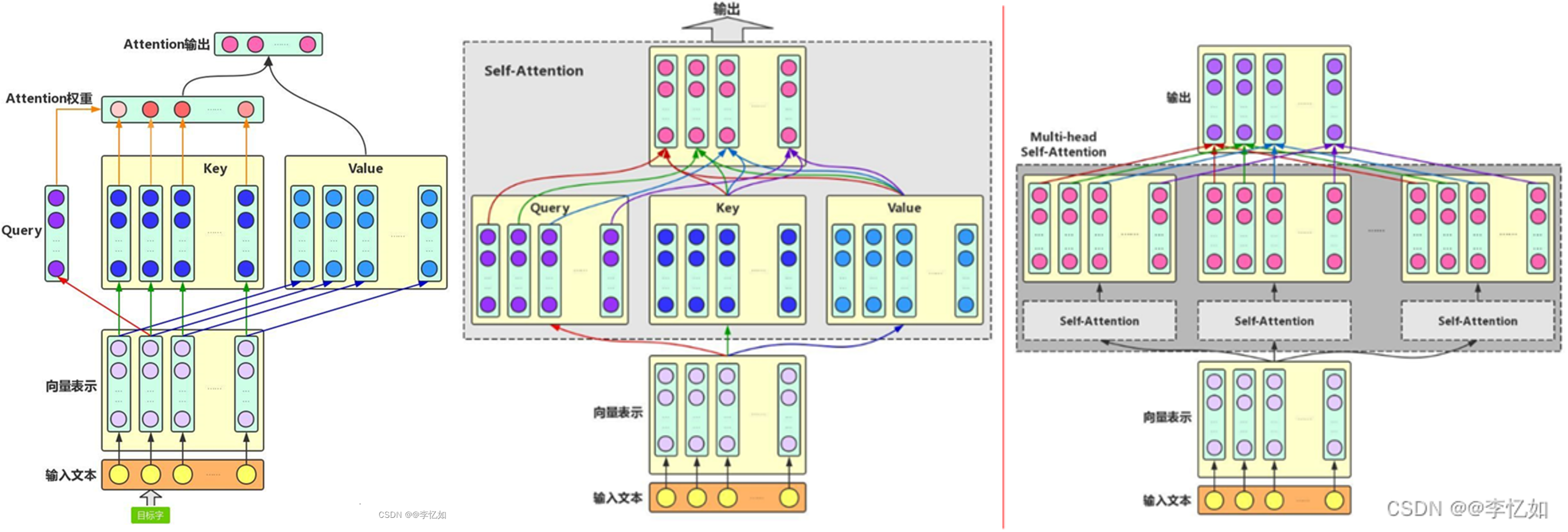
上图为注意力架构参考:普通注意力、Self-Attention与Multi-head Attention
从GNN到GCN再到GAT:
- GNN:权重依靠人为设定或学习得到
- GCN:依赖于图结构决定更新权重。$H^{(l+1)}=\sigma(\hat{D}^{−1/2}\hat{A}\hat{D}^{−1/2}H^{(l)}W^{(l)})$
- GAT:GAT是对于GCN在邻居权重分配问题上的改进。注意力通过Multi-head Attention 进行学习,相比于GCN的更新权重纯粹依赖于图结构更具有合理性。
贡献:
- 引入masked self-attentional layers 来改进前面图卷积graph convolution的缺点
- 对不同的相邻节点分配相应的权重,既不需要矩阵运算,也不需要事先知道图结构
- 四个数据集上达到SOTA的准确率
相关工作
GCN是处理transductive任务的一把利器(transductive任务是指:训练阶段与测试阶段都基于同样的图结构),然而GCN有两大局限性是经常被诟病的:
- 无法完成inductive任务,即处理动态图问题。inductive任务是指:训练阶段与测试阶段需要处理的graph不同。通常是训练阶段只是在子图(subgraph)上进行,测试阶段需要处理未知的顶点。(unseen node)
- 处理有向图的瓶颈,不容易实现分配不同的学习权重给不同的neighbor。
相比于传统的图卷积网络,GAT具有以下优势:
- 适用于inductive任务:传统的图卷积网络擅长处理transductive任务,而无法完成inductive任务。而GAT仅需要一阶邻居节点的信息,因此可以处理更广泛的图数据,实现inductive任务。
- 不同邻居节点的权重学习:传统的图卷积网络对于同一个节点的不同邻居在卷积操作时使用相同的权重,而GAT通过注意力机制允许为不同的邻居节点学习不同的权重。这使得GAT可以更精确地捕捉节点之间的重要关系,提高了模型的表现能力。
我们可以发现本质上而言:GCN与GAT都是将邻居顶点的特征聚合到中心顶点上(一种aggregate运算),利用graph上的local stationary学习新的顶点特征表达。不同的是GCN利用了拉普拉斯矩阵,GAT利用attention系数。一定程度上而言,GAT会更强,因为 顶点特征之间的相关性被更好地融入到模型中。
此外,GCN是一种全图的计算方式,一次计算就更新全图的节点特征。学习的参数很大程度与图结构相关,这使得GCN在inductive任务上遇到困境。而GAT中重要的学习参数是 W 和 a ,因为逐顶点运算方式,这两个参数仅与顶点特征相关,与图的结构毫无关系。所以测试任务中改变图的结构,对于GAT影响并不大,只需要改变邻居 $\mathcal{N}_i$ 重新计算即可。
模型
注意力机制
注意力机制是深度神经网络(DNN)中的一种重要机制,其灵感来源于人类处理信息的方式。由于人类的信息处理能力有限,我们往往会选择性地关注信息的一部分,忽略其他不太重要的信息。
类似地,注意力机制的目标是对给定的信息进行权重分配,将注意力集中在对系统来说最重要的信息上,从而使得网络可以更加关注重要的部分并进行重点加工。
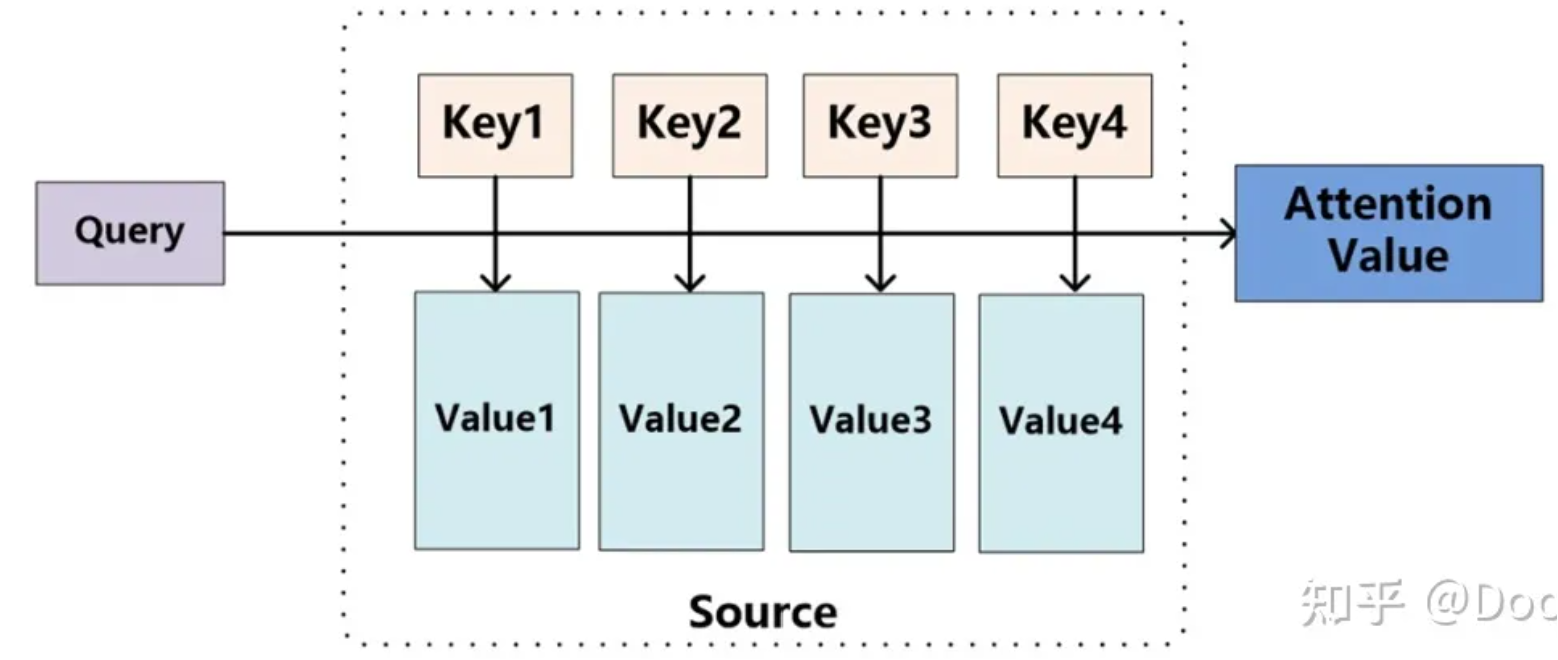
Attention函数的本质可以被描述为一个查询(query)到一系列(键key-值value)对的映射。
其中,有一个待处理的信息源Source和一个表示条件或先验信息的Query。信息源中包含多种信息,我们将每种信息都表示成键值对(Key-Value)的形式,其中Key表示信息的关键信息,Value表示该信息的具体内容。注意力机制的目标是根据Query,从信息源Source中提取与Query相关的信息,即Attention Value。
\[Attention(Query,Source)=\sum_isimilarity(Query, Key_i)\cdot Value_i\]上式中Query,Key,Value,Attention Value在实际计算时均可以是向量形式。相关度最直接的方法是可以取两向量的内积(用内积去表示两个向量的相关度是DNN里面常用的方法,对于两个单位向量,如果内积接近1,代表两向量接近重合,相似度就高)。
计算注意力系数(attention coefficient)
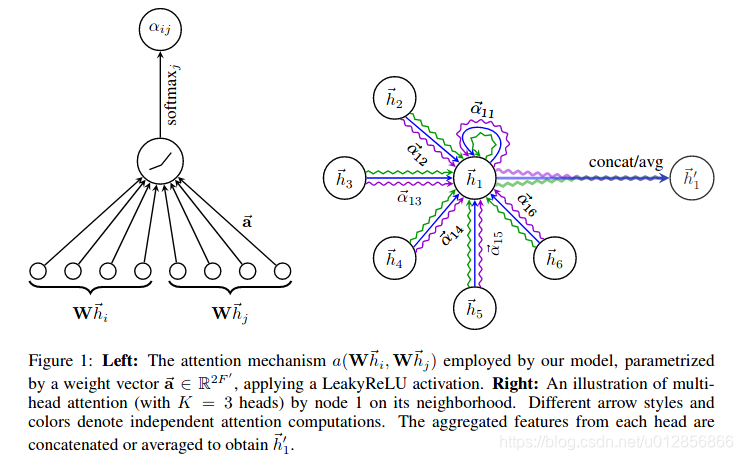
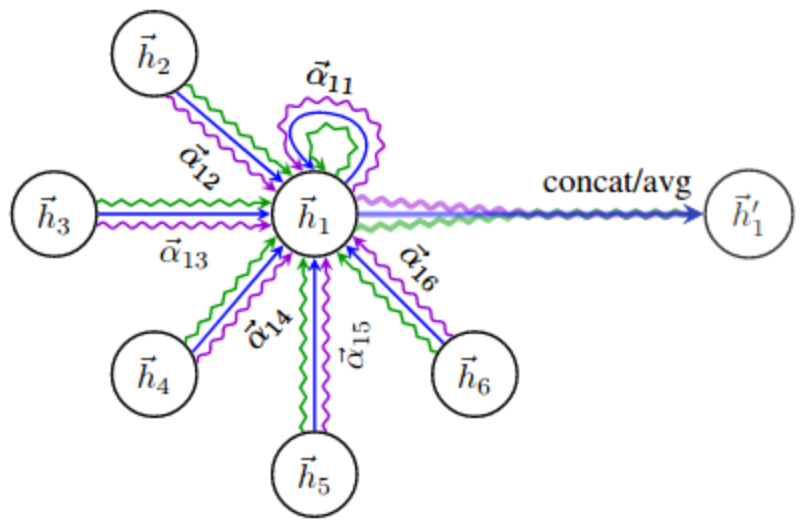
结合上图,GAT的核心思想就是针对节点 i 和节点 j,GAT首先学习了他们之间的注意力权重 $a_{i,j}$(如左图所示),然后,基于注意力权重 ${a_1, … , a_6}$ 来对节点 ${1, 2, … ,6}$ 的表示 ${h_1, … , h_6}$ 加权平均,进而得到节点1的表示 ${h}’_1$
对于顶点 i ,有顶点自己的特征 $h_i$,有它在图上邻居 $\mathcal{N}_i$, 逐个计算它的邻居们和它自己之间的相似系数:
\[e_{ij} =a\left( \left[ Wh_i \big| \big| Wh_j \right] \right),j \in \mathcal{N}_i\]解读一下这个公式:
- 首先一个共享参数 W的线性映射对于顶点的特征进行了增维,当然这是一种常见的特征增强(feature augment)方法
- 对于顶点 i,j 的变换后的特征进行了拼接(concatenate) \(\left[ \cdot \big| \big| \cdot\right]\)
- 最后 $a(\cdot)$ 把拼接后的高维特征映射到一个实数上,作者是通过 single-layer feedforward neural network实现的。
有了相关系数,离注意力系数就差归一化了!其实就是用个softmax:
\[\alpha_{ij}=\frac{\exp\left( \text{LeakyReLU}(e_{ij}) \right)}{\sum_{k\in \mathcal{N}_i}{\exp\left( \text{LeakyReLU}(e_{ik}) \right)}}\]加权求和(aggregate)
根据计算好的注意力系数,把特征加权求和(aggregate)一下。
\[h_i^{'}=\sigma\left( \sum_{j\in \mathcal{N}_i}{\alpha_{ij}W}h_j \right)\]$h_i^{‘}$就是GAT输出的对于每个顶点 i 的新特征(融合了邻域信息)
看着还有点单薄,可以加入多头注意力机制(multi-head attention),即对上式调用K组相互独立的注意力机制,然后将输出结果拼接在一起,当然,为了减少输出的特征向量的维度,可以将拼接操作替换成平均操作:
\[h_i^{'}(K)= \overset{K}{\underset{k=1}{\big| \big|}} \sigma\left( \sum_{j\in \mathcal{N}_i}{\alpha_{ij}^k W^k}h_j \right)\]多头图注意力层的优势在于能够学习多组不同的注意力机制,使得模型可以充分考虑不同节点之间的相关性和重要性。通过增加注意力头数K,可以进一步提高模型的表达能力。
到此为止,我们完成了一层GAT运算。本质上, GAT只是将原本GCN的标准化函数替换为使用注意力权重的邻居节点特征聚合函数。其余部分和普通的GCN和GNN思想相同。