Generative Adversarial Nets
读论文时间!
生成对抗网络:GAN
参考:
相关工作
生成对抗网络相比于之前一些生成式的模型,之前的一些生成式模型是要学习数据到底是什么样的一个分布,然而生成对抗网络只需要生成的东西和原来的看上去像就行,而不去管它到底是什么分布。
例如玩游戏会有游戏画面,之前的一些模型就好比要把这些游戏代码学习出来,再生成游戏画面。生成对抗网络只是模拟着画出来一个比较像的游戏画面而已。
生成对抗网络优点:
- 能更好建模数据分布(图像更锐利、清晰);
- 理论上,GANs 能训练任何一种生成器网络。其他的框架需要生成器网络有一些特定的函数形式,比如输出层是高斯的;
- 无需利用马尔科夫链反复采样,无需在学习过程中进行推断,没有复杂的变分下界,避开近似计算棘手的概率的难题。
生成对抗网络缺点:
- 模型难以收敛,不稳定。生成器和判别器之间需要很好的同步,但是在实际训练中很容易D收敛,G发散。D/G 的训练需要精心的设计。
- 模式缺失(Mode Collapse)问题。GANs的学习过程可能出现模式缺失,生成器开始退化,总是生成同样的样本点,无法继续学习。
模型
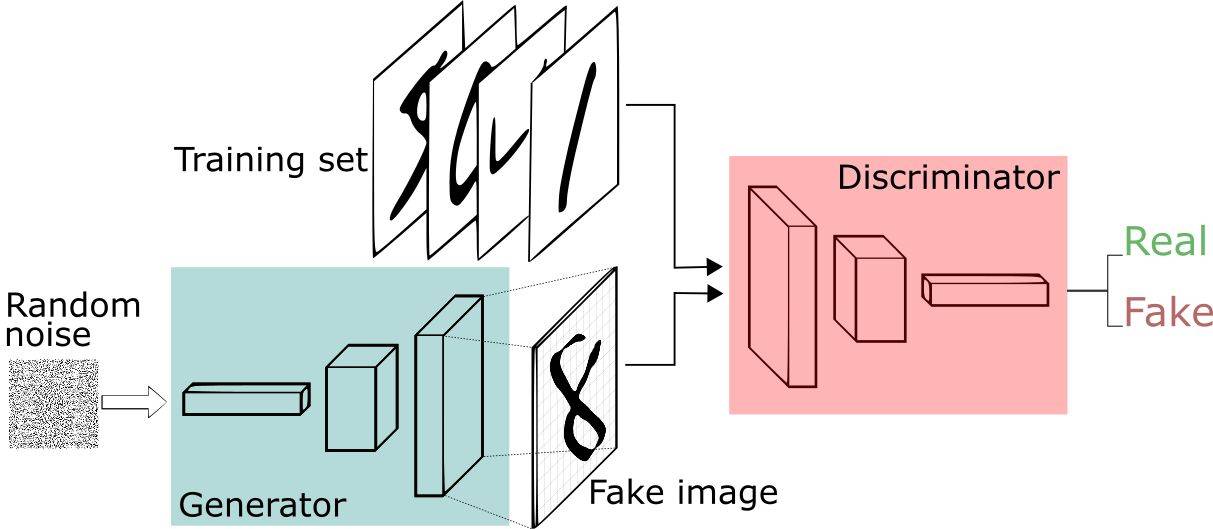
GAN由两个重要的部分构成:生成器(Generator,简写作G)和判别器(Discriminator,简写作D)。
- 生成器:通过机器生成数据,目的是尽可能“骗过”判别器,生成的数据记做G(z);
- 判别器:判断数据是真实数据还是「生成器」生成的数据,目的是尽可能找出「生成器」造的“假数据”。它的输入参数是x,x代表数据,输出D(x)代表x为真实数据的概率,如果为1,就代表100%是真实的数据,而输出为0,就代表不可能是真实的数据。
这样,G和D构成了一个动态对抗(或博弈过程),随着训练(对抗)的进行,G生成的数据越来越接近真实数据,D鉴别数据的水平越来越高。在理想的状态下,G可以生成足以“以假乱真”的数据;而对于D来说,它难以判定生成器生成的数据究竟是不是真实的,因此D(G(z)) = 0.5。训练完成后,我们得到了一个生成模型G,它可以用来生成以假乱真的数据。
博弈过程可以用以下公式在数学上描述。
\[\min_G \max_D V(G,D) = \mathbb{E}_{x\sim p_{data}(x)}[\log D(x)] + \mathbb{E}_{z\sim p_{z}(z)}[\log (1-D(G(z))]\]- 其中,G 代表生成器;
- D 代表鉴别器;
- $p_{data}(x)$ 代表真实数据的分布;
- x 代表服从 $p_{data}(x)$ 的样本
- $p_{z}(z)$ 代表噪声的分布;
- z 代表服从 $p_{z}(z)$的样本。
对于判别器D,它的理想状态是:将真的数据判别成1,将生成的数据判别成0,所以他希望最大化这个价值函数。在D是完美的情况下,价值函数的两项都等于0。
对于生成器G,它的理想状态是:它生成的数据尽可能类似于真的数据,已因此要把这个式子最小化,让价值函数变成负数。这样构成了一个动态对抗
训练
- 找到一些真实的数据,和一些噪声,根据上面的公式训练辨别器。
- 找到一些噪声,根据上面的公式训练生成器,这里注意,因为价值函数中的前半部分和生成器无关,所以在这可以去掉。
- 循环。
这个模型是比较难训练的:
- 其一是因为价值函数是一个博弈过程,有时会变大有时会变小,所以不好判断什么时候模型能够收敛。
- 第二个原因是因为,如果辨别器和生成器两者的能力出现了有较大的差别,就不会很好的训练下去。
第二点可以这么想:假设生成器是卖假货的,辨别器是警察。如果说警察特别厉害,那么卖假货的一旦造出点假货就被连窝一起端掉了,但是如果警察能力很一般,那么造假者也没有动力去更新他的工艺。
训练过程的直观解释如下:
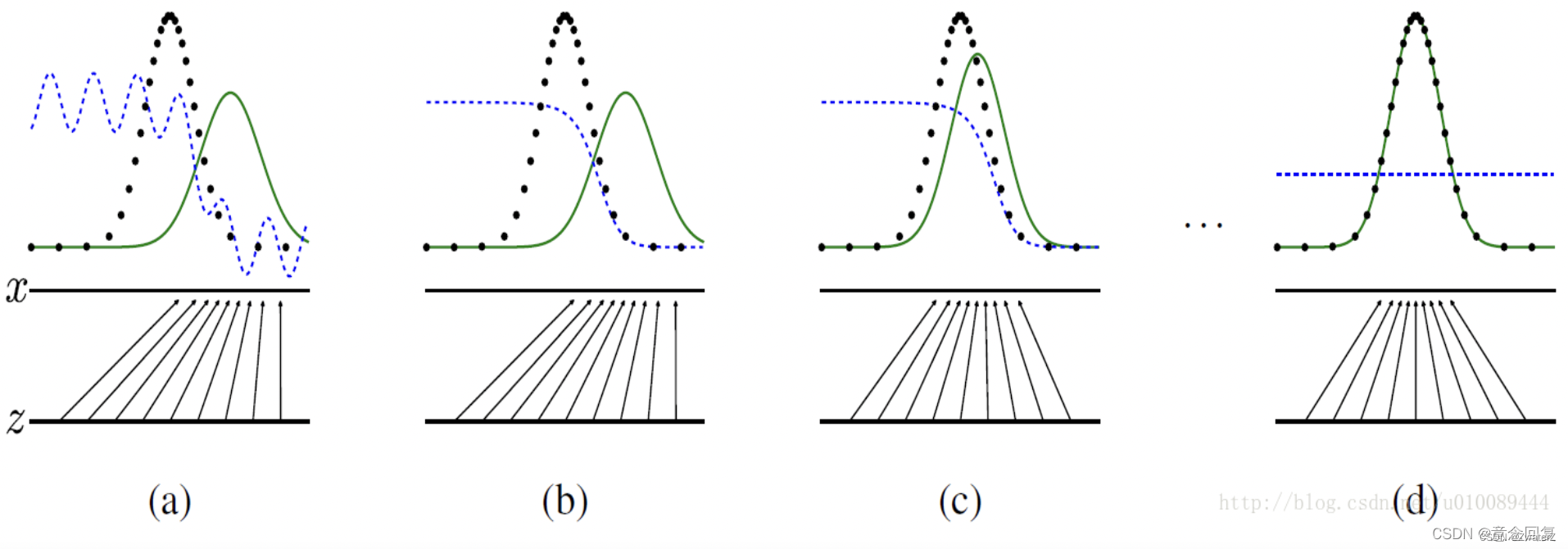
其中,蓝色虚线为判别模型D的分布,黑色虚线为真实数据的分布Pdata,绿色实线为生成模型G学习的分布Pg。下方的水平线为均匀采样噪声z的区域,上方的水平线为数据x的区域。朝上的箭头表示将随机噪声转化成数据,即x=G(z)。
从图(a)到图(b)给出了一个GANs的收敛过程。
- 图(a)中,Pg与Pdata存在相似性,但还未完全收敛,D是个部分准确的分类器。
- 图(b)中,分类器已经训练到了一个比较好的程度,它能明显的分别黑色虚线和绿色虚线。
- 图(c)中,对G进行了更新,D的梯度引导G(z)移向更可能分类为真实数据的区域。
- 图(d)中,训练若干步后,若G和D均有足够的capacity,它们接近某个稳定点,此时Pg=Pdata。判别模型将无法区分真实数据分布和生成数据分布,即D(x)=0.5。