Deep Residual Learning for Image Recognition

读论文时间！
计算机视觉模型：ResNet
参考：吴恩达深度学习视频

吴恩达说残差网络

非常非常深的神经网络是很难训练的，因为存在梯度消失和梯度爆炸问题。这节课我们学习跳跃连接（Skip connection），它可以从某一层网络层获取激活，然后迅速反馈给另外一层，甚至是神经网络的更深层。利用跳跃连接构建能够训练深度网络的残差网络（ResNet），有时深度能够超过100层。

回忆一下$a^{[l]}$到$a^{[l+2]}$的计算过程：
\[\begin{align} \left\{ \begin{aligned} z^{\left\lbrack l + 1 \right\rbrack} = W^{\left\lbrack l + 1 \right\rbrack}a^{[l]} + b^{\left\lbrack l + 1 \right\rbrack} \\ a^{\left\lbrack l + 1 \right\rbrack} =g(z^{\left\lbrack l + 1 \right\rbrack})\\ z^{\left\lbrack l + 2 \right\rbrack} = W^{\left\lbrack l+2 \right\rbrack}a^{\left\lbrack l + 1 \right\rbrack} + b^{\left\lbrack l + 2 \right\rbrack}\\ a^{\left\lbrack l + 2 \right\rbrack} = g(z^{\left\lbrack l + 2 \right\rbrack}) \end{aligned} \right. \end{align}\]

在残差网络中有一点变化，在$a^{[l]}$到$a^{[l+2]}$的计算过程更改如下：

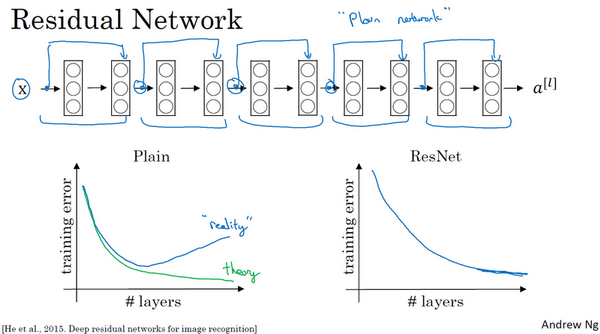
\[\begin{align} \left\{ \begin{aligned} z^{\left\lbrack l + 1 \right\rbrack} = W^{\left\lbrack l + 1 \right\rbrack}a^{[l]} + b^{\left\lbrack l + 1 \right\rbrack} \\ a^{\left\lbrack l + 1 \right\rbrack} =g(z^{\left\lbrack l + 1 \right\rbrack})\\ z^{\left\lbrack l + 2 \right\rbrack} = W^{\left\lbrack l+2 \right\rbrack}a^{\left\lbrack l + 1 \right\rbrack} + b^{\left\lbrack l + 2 \right\rbrack}\\ \ a^{\left\lbrack l + 2 \right\rbrack} = g\left(z^{\left\lbrack l + 2 \right\rbrack} + a^{[l]}\right) \end{aligned} \right. \end{align}\]

把一个普通网络（Plain network）变成ResNet的方法是加上跳跃连接，如同下面这张图，每两层增加一个捷径，构成一个残差块，5个残差块连接在一起构成一个残差网络。

如果我们使用标准优化算法训练一个普通网络，比如说梯度下降法，没有加上残差，凭经验会发现随着网络深度的加深，训练错误会先减少，然后增多。（尽管理论上，随着网络深度的加深，应该训练得越来越好才对）

ResNets确实在训练深度网络方面非常有效，它确实有助于解决梯度消失和梯度爆炸问题，让我们在训练更深网络的同时，又能保证良好的性能。

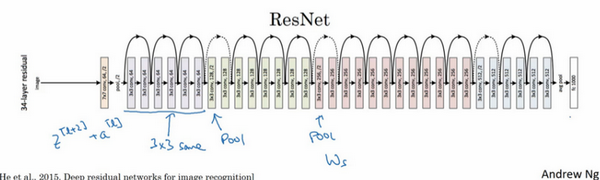
一个图片识别的ResNet例子：

论文省流版

1. Introduction

网络深度十分重要，然而主流的“深层”网络（只）包含16到30层。

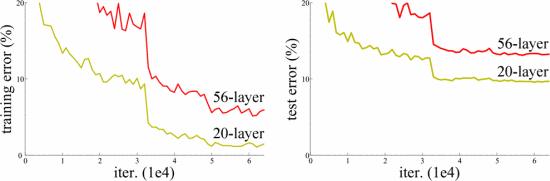
如图，一个困境是对于朴素的神经网络，当深度到达一定程度时，更深的网络反而误差更大。原因来自于梯度消失与梯度爆炸。

ResNet希望对于一个更深的网络，其误差要比浅层版本要低。

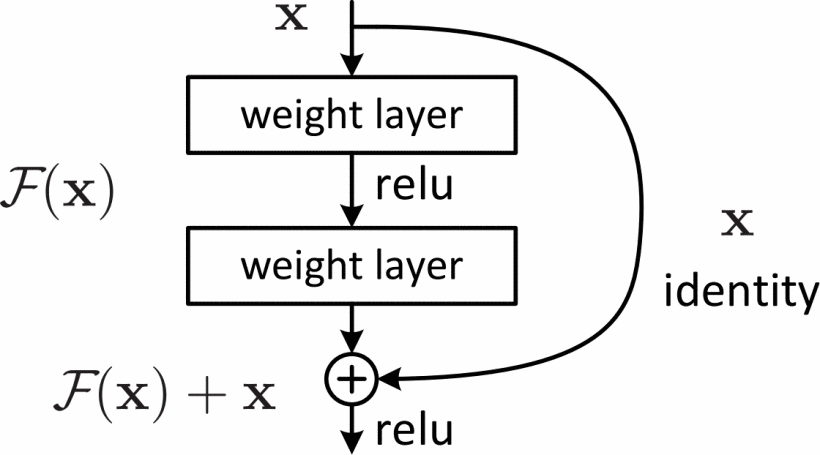
这是一个基本模块，ResNet由这种基本模块堆叠构成。

在ImageNet数据集上实验后，ResNet的优点包括：

容易优化，比朴素网络的误差更低。
能够充分享受到深层网络的优势。

之前的工作告诉我们，良好的重新制定或预处理可以简化优化过程。

相比“highway networks”，ResNet的基本模块是无参的，没有“门”的概念，门也不会关闭，并且能将层数做得更多。

3. Deep Residual Learning

在朴素的网络中，我们假设某几层要学习$\mathcal{H}(\text{x})$。而上图中的ResNet基本模块中，添加了一条“捷径”，那些层本身要学习的变成了：$\mathcal{F}(\text{x}):=\mathcal{H}(\text{x})-\text{x}$

这样，在通过捷径加入$\text{x}$后，又变回了原来的$\mathcal{H}(\text{x})$。

这种操作有效的原因是，基本模块在什么也不做只是传递$\text{x}$时，即$\mathcal{F}(\text{x})=0$，就退化成了层数更少，更简单的网络，理论上误差不会比浅层网络更大。

相比与朴素的网络，ResNet训练$\mathcal{H}(\text{x})=\text{x}$更简单，因为只需要让$\mathcal{F}(\text{x})$的参数$W=0$。

如果用公式总结ResNet基本模块，（并且$\mathcal{F}$与$\text{x}$维度一样）可以这么写：

\[\text{y}=\mathcal{F}(\text{x},\{W_i\})+\text{x} \tag{1}\]

在上图示例中使用了两层，所以$\mathcal{F}=W_2\sigma(W_1\text{x})$

如果$\mathcal{F}$与$\text{x}$维度不一致，公式可以修改为：

\[\text{y}=\mathcal{F}(\text{x},\{W_i\})+W_s\text{x} \tag{2}\]

作者建议只在使用维度匹配时加入参数$W_2$，因为实验证明不加参数$W_2$性能已经足够。

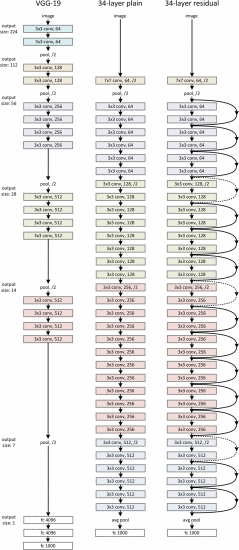
如上图，分别是VGG-19，朴素网络与残差网络。注意虽然看上去VGG-19更简单，残差网络的参数量是更少的。

残差网络的设计有两个特点：

同一个基本模块的过滤器数量相同。
特征矩阵每次减半，过滤器数量翻倍。

4. Experiments

对于ImageNet数据集的实验证明RetNet很棒，三个原因：

对于RetNet更深的网络，其误差要比浅层版本要低。
在深层学习中残差学习很高效。
更快收敛。

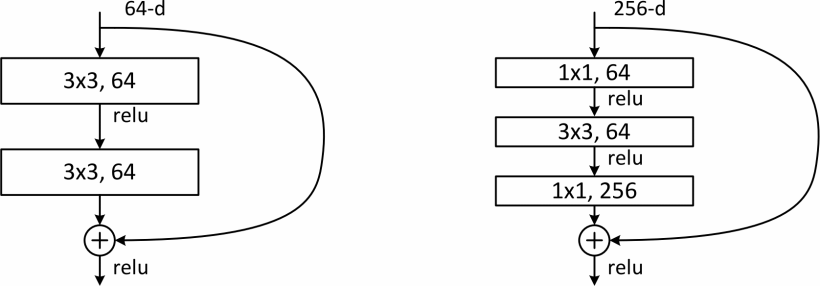
为了训练经济考虑（在有限的计算资源下缩短训练时间），论文作者引入了瓶颈层。如下图右侧，两个1x1的卷积层负责降维和升维，所以留给3x3卷积层计算的数据可以变少。

注意引入瓶颈层会使准确率下降（原因与朴素网络相同），引入的理由只是训练经济考虑。

代码分析

代码来自PyTorch中torchvision的ResNet。

以最简单的ResNet18为例，初始化并且打印网络结构：

  
import torchvision

model = torchvision.models.resnet18()
print(model)

ResNet(
  (conv1): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
  (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (relu): ReLU(inplace=True)
  (maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
  (layer1): Sequential(
    (0): BasicBlock(
      (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
    (1): BasicBlock(
      (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (layer2): Sequential(
    (0): BasicBlock(
      (conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (downsample): Sequential(
        (0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
        (1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (1): BasicBlock(
      (conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (layer3): Sequential(
    (0): BasicBlock(
      (conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (downsample): Sequential(
        (0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
        (1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (1): BasicBlock(
      (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (layer4): Sequential(
    (0): BasicBlock(
      (conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (downsample): Sequential(
        (0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
        (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (1): BasicBlock(
      (conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
      (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    )
  )
  (avgpool): AdaptiveAvgPool2d(output_size=(1, 1))
  (fc): Linear(in_features=512, out_features=1000, bias=True)
)

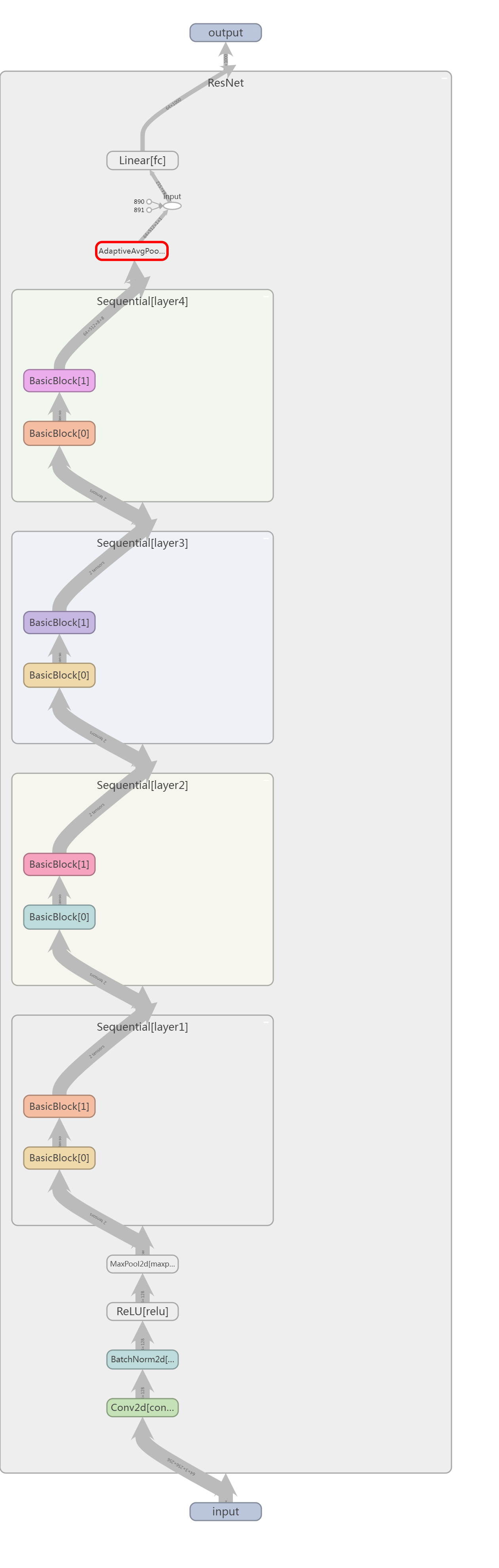
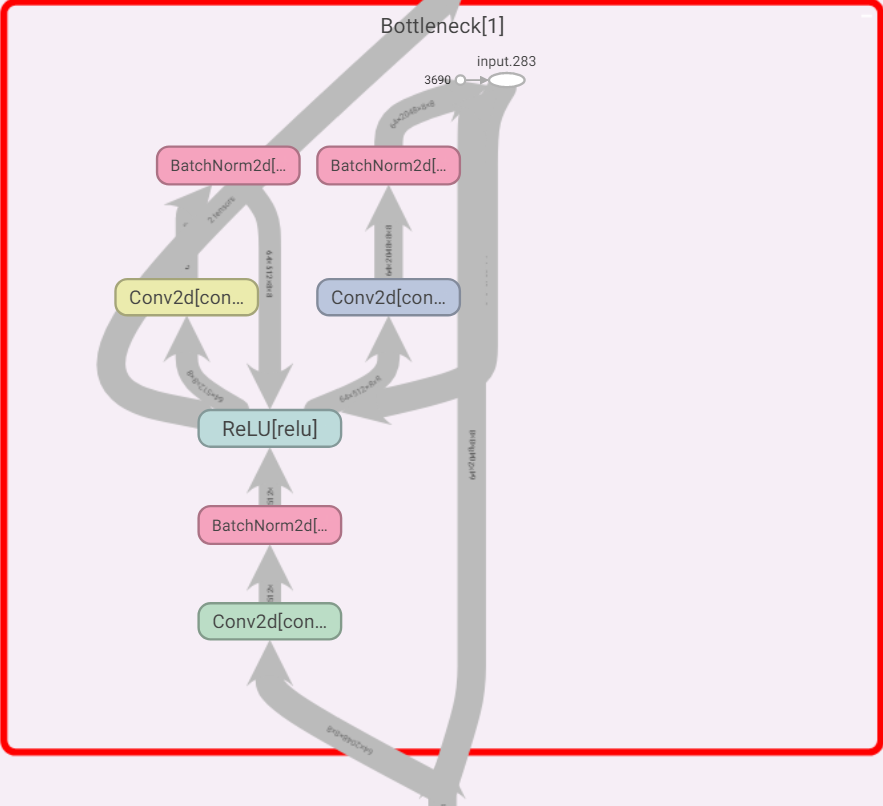
可视化版本：

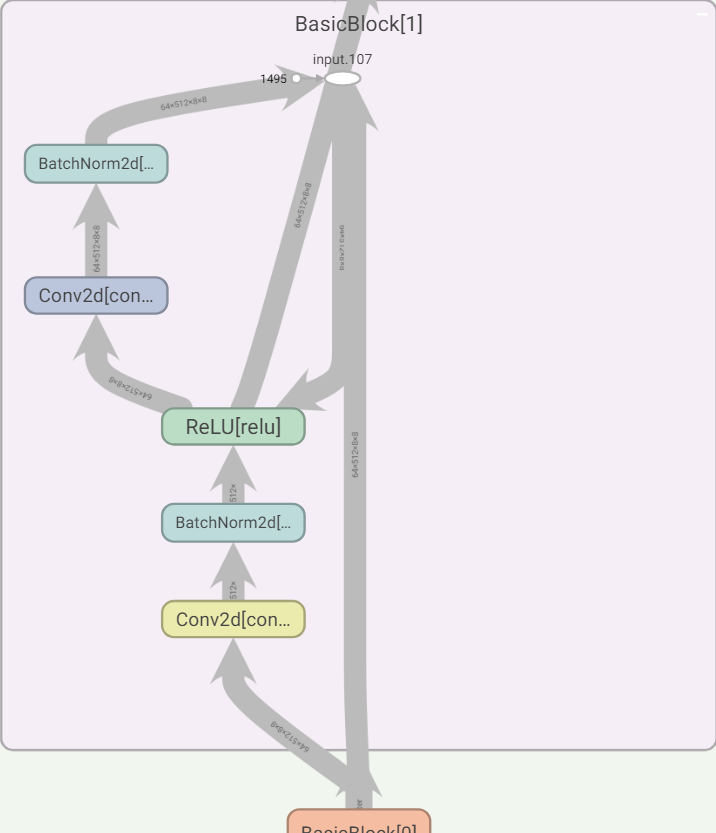
其中，一个基本模块：

现在深入torchvision源码，虽然提供了很多restet版本，比如’resnet18’, ‘resnet34’, ‘resnet50’, ‘resnet101’,’resnet152’等等，它们都由类似的函数生成：

  
def resnet18(pretrained=False, progress=True, **kwargs):
    r"""ResNet-18 model from
    `"Deep Residual Learning for Image Recognition" <https://arxiv.org/pdf/1512.03385.pdf>`_
    Args:
        pretrained (bool): If True, returns a model pre-trained on ImageNet
        progress (bool): If True, displays a progress bar of the download to stderr
    """
    return _resnet('resnet18', BasicBlock, [2, 2, 2, 2], pretrained, progress,
                   **kwargs)

通过观察上面打印的网络结构，都有layer1，layer2，layer3，layer4，它们的结构不同是’resnet18’, ‘resnet34’, ‘resnet50’, ‘resnet101’,’resnet152’各个版本区分的本质，这由参数[2, 2, 2, 2]决定。

BasicBlock是一个类，就是论文中提到的基本模块。

而_resnet是什么呢？

  
def _resnet(arch, block, layers, pretrained, progress, **kwargs):
    model = ResNet(block, layers, **kwargs)
    if pretrained:
        state_dict = load_state_dict_from_url(model_urls[arch],
                                              progress=progress)
        model.load_state_dict(state_dict)
    return model

其中核心语句model = ResNet(block, layers, **kwargs)，block是BasicBlock，layers是参数[2, 2, 2, 2]。

终于到我们的ResNet类了，看看__init__函数，不太重要的语句去除了：

  
class ResNet(nn.Module):

    def __init__(self, block, layers, num_classes=1000, zero_init_residual=False,
                 groups=1, width_per_group=64, replace_stride_with_dilation=None,
                 norm_layer=None):
        super(ResNet, self).__init__()
        if norm_layer is None:
            norm_layer = nn.BatchNorm2d
        self._norm_layer = norm_layer

        self.inplanes = 64
        self.dilation = 1
        self.groups = groups
        self.base_width = width_per_group
        self.conv1 = nn.Conv2d(3, self.inplanes, kernel_size=7, stride=2, padding=3,
                               bias=False)
        self.bn1 = norm_layer(self.inplanes)
        self.relu = nn.ReLU(inplace=True)
        self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
        self.layer1 = self._make_layer(block, 64, layers[0])
        self.layer2 = self._make_layer(block, 128, layers[1], stride=2,
                                       dilate=replace_stride_with_dilation[0])
        self.layer3 = self._make_layer(block, 256, layers[2], stride=2,
                                       dilate=replace_stride_with_dilation[1])
        self.layer4 = self._make_layer(block, 512, layers[3], stride=2,
                                       dilate=replace_stride_with_dilation[2])
        self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
        self.fc = nn.Linear(512 * block.expansion, num_classes)

我们可以对照上面打印的网络结构基本理解各层，除了生成layer1，layer2，layer3，layer4的_make_layer函数，来看看，本质上就是添加layers[i]个基本模块：

  
def _make_layer(self, block, planes, blocks, stride=1, dilate=False):
    norm_layer = self._norm_layer
    downsample = None
    previous_dilation = self.dilation
    if dilate:
        self.dilation *= stride
        stride = 1
    if stride != 1 or self.inplanes != planes * block.expansion:
        downsample = nn.Sequential(
            conv1x1(self.inplanes, planes * block.expansion, stride),
            norm_layer(planes * block.expansion),
        )

    layers = []
    layers.append(block(self.inplanes, planes, stride, downsample, self.groups,
                        self.base_width, previous_dilation, norm_layer))
    self.inplanes = planes * block.expansion
    for _ in range(1, blocks):
        layers.append(block(self.inplanes, planes, groups=self.groups,
                            base_width=self.base_width, dilation=self.dilation,
                            norm_layer=norm_layer))

    return nn.Sequential(*layers)

对于两个残差块之间可能维度不匹配无法直接相加的问题，相同类型的残差块只需要改变第一个输入的维数就好，后面的输入维数都等于输出维数。第一残差块需特判。

基本模块代码：

  
class BasicBlock(nn.Module):
    expansion = 1

    def __init__(self, inplanes, planes, stride=1, downsample=None, groups=1,
                 base_width=64, dilation=1, norm_layer=None):
        super(BasicBlock, self).__init__()
        if norm_layer is None:
            norm_layer = nn.BatchNorm2d
        if groups != 1 or base_width != 64:
            raise ValueError('BasicBlock only supports groups=1 and base_width=64')
        if dilation > 1:
            raise NotImplementedError("Dilation > 1 not supported in BasicBlock")
        # Both self.conv1 and self.downsample layers downsample the input when stride != 1
        self.conv1 = conv3x3(inplanes, planes, stride)
        self.bn1 = norm_layer(planes)
        self.relu = nn.ReLU(inplace=True)
        self.conv2 = conv3x3(planes, planes)
        self.bn2 = norm_layer(planes)
        self.downsample = downsample
        self.stride = stride

    def forward(self, x):
        identity = x

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)

        if self.downsample is not None:
            identity = self.downsample(x)

        out += identity
        out = self.relu(out)

        return out

其中，conv3x3就是3x3的卷积层：

  
def conv3x3(in_planes, out_planes, stride=1, groups=1, dilation=1):
    """3x3 convolution with padding"""
    return nn.Conv2d(in_planes, out_planes, kernel_size=3, stride=stride,
                     padding=dilation, groups=groups, bias=False, dilation=dilation)

norm_layer默认使用nn.BatchNorm2d，即对小批量(mini-batch)3d数据（即通道加2d数据）组成的4d输入（即batch-size，通道加2d数据）进行批标准化(Batch Normalization)操作，在每一个小批量（mini-batch）数据中，计算输入各个维度的均值和标准差。gamma与beta是可学习的大小为C的参数向量（C为输入大小）在训练时，该层计算每次输入的均值与方差，并进行移动平均。移动平均默认的动量值为0.1。

\[y = \frac{x - mean[x]}{ \sqrt{Var[x]} + \epsilon} * gamma + beta\]

对于 ‘resnet50’, ‘resnet101’,’resnet152’，基本模块就变成了瓶颈层：

  
class Bottleneck(nn.Module):
    # Bottleneck in torchvision places the stride for downsampling at 3x3 convolution(self.conv2)
    # while original implementation places the stride at the first 1x1 convolution(self.conv1)
    # according to "Deep residual learning for image recognition"https://arxiv.org/abs/1512.03385.
    # This variant is also known as ResNet V1.5 and improves accuracy according to
    # https://ngc.nvidia.com/catalog/model-scripts/nvidia:resnet_50_v1_5_for_pytorch.

    expansion = 4

    def __init__(self, inplanes, planes, stride=1, downsample=None, groups=1,
                 base_width=64, dilation=1, norm_layer=None):
        super(Bottleneck, self).__init__()
        if norm_layer is None:
            norm_layer = nn.BatchNorm2d
        width = int(planes * (base_width / 64.)) * groups
        # Both self.conv2 and self.downsample layers downsample the input when stride != 1
        self.conv1 = conv1x1(inplanes, width)
        self.bn1 = norm_layer(width)
        self.conv2 = conv3x3(width, width, stride, groups, dilation)
        self.bn2 = norm_layer(width)
        self.conv3 = conv1x1(width, planes * self.expansion)
        self.bn3 = norm_layer(planes * self.expansion)
        self.relu = nn.ReLU(inplace=True)
        self.downsample = downsample
        self.stride = stride

    def forward(self, x):
        identity = x

        out = self.conv1(x)
        out = self.bn1(out)
        out = self.relu(out)

        out = self.conv2(out)
        out = self.bn2(out)
        out = self.relu(out)

        out = self.conv3(out)
        out = self.bn3(out)

        if self.downsample is not None:
            identity = self.downsample(x)

        out += identity
        out = self.relu(out)

        return out

  
(1): Bottleneck(
      (conv1): Conv2d(64, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
      (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (conv3): Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
      (bn3): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      (relu): ReLU(inplace=True)
    )

Deep Residual Learning for Image Recognition

吴恩达说残差网络

论文省流版

1. Introduction

2. Related Work

3. Deep Residual Learning

4. Experiments

代码分析

相关文章

Multitask learning and benchmarking with clinical time series data

Attention Is All You Need

An Image Is Worth 16x16 Words： Transformers For Image Recognition At Scale