首页 Attention Is All You Need
文章
取消

Attention Is All You Need

发表于 2024/01/24 更新于 2024/07/17
作者 赛博升哥
42 分钟阅读

读论文时间！

  • 原文名称：Attention Is All You Need
  • 原文链接：https://arxiv.org/abs/1706.03762

参考：

  • https://blog.csdn.net/weixin_42475060/article/details/121101749
  • https://www.bilibili.com/read/cv13759416
  • https://blog.csdn.net/qq_37541097/article/details/117691873
  • https://b23.tv/gucpvt
  • 《大规模语言模型从理论到实践》

在学习完之后，推荐参考llm可视化的例子看看是否真正了解了每一步的计算过程。

由于RNN将前一个节点的输出作为下一个阶段输入，所以每次只能处理一个，不能并行处理所有节点。

Transformer改进了RNN训练比较慢的缺点，利用self-attention机制实现了快速的并行运算。并且最早，Transformer是用于翻译任务的。不过后续 BERT 的使用以及图片、视频的应用让 Transformer 出圈了。

0、整体介绍

先将模型图放在这，并且做整体介绍，细节下面讲解。

0.1、Encoder & Decoder

encoder 将 $(x_1, x_2, … , x_n)$（原始输入） 映射成 $(z_1, z_2, … , z_n)$（机器学习可以理解的向量）i.e., 一个句子有 n 个词，$x_t$ 是第 t 个词，$z_t$ 是第 t 个词的向量表示。

decoder 拿到 encoder 的输出，会生成一个长为 m 的序列 $(y_1, y_2, … , y_m)$。n 和 m 可以一样长、可以不一样长。

encoder 和 decoder 的区别：encoder 一次性可以看全整个句子。i.e., 翻译的时候，看到整句英语：Hello World。decoder 在解码的时候，输出词只能一个一个的生成。过去时刻的输出会作为你当前时刻的输入，自回归 auto-regressive。

decoder在做预测的时候 是没有输入的。Shifted right 指的是 decoder 在之前时刻的一些输出，作为此时的输入。一个一个往右移。

在做预测时，步骤如下：

  1. 给 decoder 输入 encoder 对整个句子 embedding 的结果 和一个特殊的开始符号 </s>。decoder 将产生预测，在我们的例子中应该是 ”为”。
  2. 给 decoder 输入 encoder 的 embedding 结果和 “</s>为”，在这一步 decoder 应该产生预测 “什”。
  3. 给 decoder 输入 encoder 的 embedding 结果和 “</s>为什”，在这一步 decoder 应该产生预测 “么”。
  4. 给 decoder 输入 encoder 的 embedding 结果和 “</s>为什么”，在这一步 decoder 应该产生预测 “要”
  5. 给 decoder 输入 encoder 的 embedding 结果和 “</s>为什么要”，在这一步 decoder 应该产生预测 “工”。
  6. 给 decoder 输入 encoder 的 embedding 结果和 “</s>为什么要工”，在这一步 decoder 应该产生预测 “作”。
  7. 给 decoder 输入 encoder 的 embedding 结果和 “</s>为什么要工作”, decoder应该生成句子结尾的标记，decoder 应该输出 ”</eos>”。
  8. 然后 decoder 生成了 </eos>，翻译完成。

0.2、Encoder 的核心架构

Nx：N个 Transformer 的 block 叠在一起。

Transformer 的block：

  • Multi-Head attention
  • Add & Norm: 残差连接 + Layernorm
  • Feed Forward: 前馈神经网络 MLP

每个 layer 有 2 个 sub-layers。

  • 第一个 sub-layer 是 multi-head self-attention
  • 第二个 sub-layer 是 simple, position-wise fully connected feed-forward network, 其实就是 MLP

每个 sub-layer 的输出做 残差连接 和 LayerNorm

公式：$LayerNorm( x + Sublayer(x) )$。Sublayer(x) 指 self-attention 或者 MLP

residual connections 需要输入输出维度一致，不一致需要做投影。简单起见，固定 每一层的输出维度dmodel = 512。它是一个简单设计：只需调 2 个参数 $d_{model}$ 每层维度有多大 和 N 多少层，影响后续一系列网络的设计，BERT、GPT。

编码器的示例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class EncoderLayer(nn.Module):
    def __init__(self, d_model, heads, dropout=0.1):
        super().__init__()
        self.norm_1 = Norm(d_model)  # 层归一化
        self.norm_2 = Norm(d_model)
        self.attn = MultiHeadAttention(heads, d_model, dropout=dropout)  # 多头注意力
        self.ff = FeedForward(d_model, dropout=dropout)  # 前馈网络
        self.dropout_1 = nn.Dropout(dropout)
        self.dropout_2 = nn.Dropout(dropout)

    def forward(self, x, mask):
        x2 = self.norm_1(x)
        x = x + self.dropout_1(self.attn(x2,x2,x2,mask))
        x2 = self.norm_2(x)
        x = x + self.dropout_2(self.ff(x2))
        return x
    
class Encoder(nn.Module):
    def __init__(self, vocab_size, d_model, N, heads, dropout):
        super().__init__()
        self.N = N
        self.embed = Embedder(vocab_size, d_model)  # 嵌入层
        self.pe = PositionalEncoder(d_model, dropout=dropout)  # 位置编码

        # get_clones() 函数返回 N 个相同的层
        self.layers = get_clones(EncoderLayer(d_model, heads, dropout), N)
        self.norm = Norm(d_model)
        
    def forward(self, src, mask):
        x = self.embed(src)
        x = self.pe(x)
        for i in range(self.N):
            x = self.layers[i](x, mask)
        return self.norm(x)

0.3、Decoder 的核心架构

decoder 和 encoder 很像，6个相同 layer 的堆叠，每个sub-layer 有 residual connections、layer normalization。decoder 多了一个 Masked Multi-Head Attention。

decoder的输出进入一个 Linear 层，做一个 softmax，得到输出。Linear + softmax 是一个标准的神经网络的做法 。

解码器的每个 Transformer 块的第一个自注意力子层额外增加了注意力掩码。这主要是因为在 翻译的过程中，编码器端主要用于编码源语言序列的信息，而这个序列是完全已知的，因而编码 器仅需要考虑如何融合上下文语义信息即可。而解码端则负责生成目标语言序列，这一生成过程 是自回归的，即对于每一个单词的生成过程，仅有当前单词之前的目标语言序列是可以被观测的， 因此这一额外增加的掩码是用来掩盖后续的文本信息，以防模型在训练阶段直接看到后续的文本 序列进而无法得到有效地训练。

decoder 是 auto-regressive 自回归。当前时刻的输入集是之前一些时刻的输出。做预测时，decoder 不能看到 之后时刻的输出，要避免这个情况的发生。它的做法是通过一个带掩码 masked 的注意力机制，保证 训练和预测时行为一致，后面会讲。

解码器端同时接收来自编码器端的输出以及当前 Transformer 块的前一个掩码注 意力层的输出。查询q是通过解码器前一层的输出进行投影的，而键k和值v是使用编码器的输出进行 投影的。它的作用是在翻译的过程当中，为了生成合理的目标语言序列需要观测待翻译的源语言 序列是什么。基于上述的编码器和解码器结构，待翻译的源语言文本，首先经过编码器端的每个 Transformer 块对其上下文语义的层层抽象，最终输出每一个源语言单词上下文相关的表示。解码 器端以自回归的方式生成目标语言文本，即在每个时间步 t，根据编码器端输出的源语言文本表 示，以及前 t − 1 个时刻生成的目标语言文本，生成当前时刻的目标语言单词。

解码器参考代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

class DecoderLayer(nn.Module):
    def __init__(self, d_model, heads, dropout=0.1):
        super().__init__()
        self.norm_1 = Norm(d_model)  # 层归一化
        self.norm_2 = Norm(d_model)
        self.norm_3 = Norm(d_model)
        self.dropout_1 = nn.Dropout(dropout)
        self.dropout_2 = nn.Dropout(dropout)
        self.dropout_3 = nn.Dropout(dropout)
        self.attn_1 = MultiHeadAttention(heads, d_model, dropout=dropout)  # 多头注意力
        self.attn_2 = MultiHeadAttention(heads, d_model, dropout=dropout)
        self.ff = FeedForward(d_model, dropout=dropout)  # 前馈神经网络

    def forward(self, x, e_outputs, src_mask, trg_mask):
        x2 = self.norm_1(x)
        x = x + self.dropout_1(self.attn_1(x2, x2, x2, trg_mask))
        x2 = self.norm_2(x)

        # 第二个多头注意力层的k, v是编码器的输出
        x = x + self.dropout_2(self.attn_2(x2, e_outputs, e_outputs, \
                                            src_mask))
        x2 = self.norm_3(x)
        x = x + self.dropout_3(self.ff(x2))
        return x
    

class Decoder(nn.Module):
    def __init__(self, vocab_size, d_model, N, heads, dropout):
        super().__init__()
        self.N = N
        self.embed = Embedder(vocab_size, d_model)
        self.pe = PositionalEncoder(d_model, dropout=dropout)
        self.layers = get_clones(DecoderLayer(d_model, heads, dropout), N)
        self.norm = Norm(d_model)

    def forward(self, trg, e_outputs, src_mask, trg_mask):
        x = self.embed(trg)
        x = self.pe(x)
        for i in range(self.N):
            x = self.layers[i](x, e_outputs, src_mask, trg_mask)
        return self.norm(x)

于是，最终基于 Transformer 的编码器和解码器结构整体实现参考代码如下：

1
2
3
4
5
6
7
8
9
10
11
12

class Transformer(nn.Module):
    def __init__(self, src_vocab, trg_vocab, d_model, N, heads, dropout):
        super().__init__()
        self.encoder = Encoder(src_vocab, d_model, N, heads, dropout)
        self.decoder = Decoder(trg_vocab, d_model, N, heads, dropout)
        self.out = nn.Linear(d_model, trg_vocab)

    def forward(self, src, trg, src_mask, trg_mask):
        e_outputs = self.encoder(src, src_mask)
        d_output = self.decoder(trg, e_outputs, src_mask, trg_mask)
        output = self.out(d_output)
        return output

1、注意力

1.1、原理

注意力函数是将 query 和 key-value 对映射成输出 output 的函数，其中所有的 query、key、value 和 output 都是一些向量。

具体来说，output 是 value 的一个加权和，权重等价于 query 和对应的 key 的相似度 ，输出的维度与 value 的维度相同。

即使 key-value 并没有变，但是随着 query 的改变，因为权重的分配不一样，导致输出会有不一样，这就是注意力机制。

Transfomer 首先将 token 映射成向量，这种多维向量本身带有信息，但还没有综合上下文信息。注意力机制可以看作让每个 token 都能够关注到其他 token 的信息，从而综合上下文。例如假期和假货的假代表不同的意义，但这种区别只有通过上下文才能体现出来。

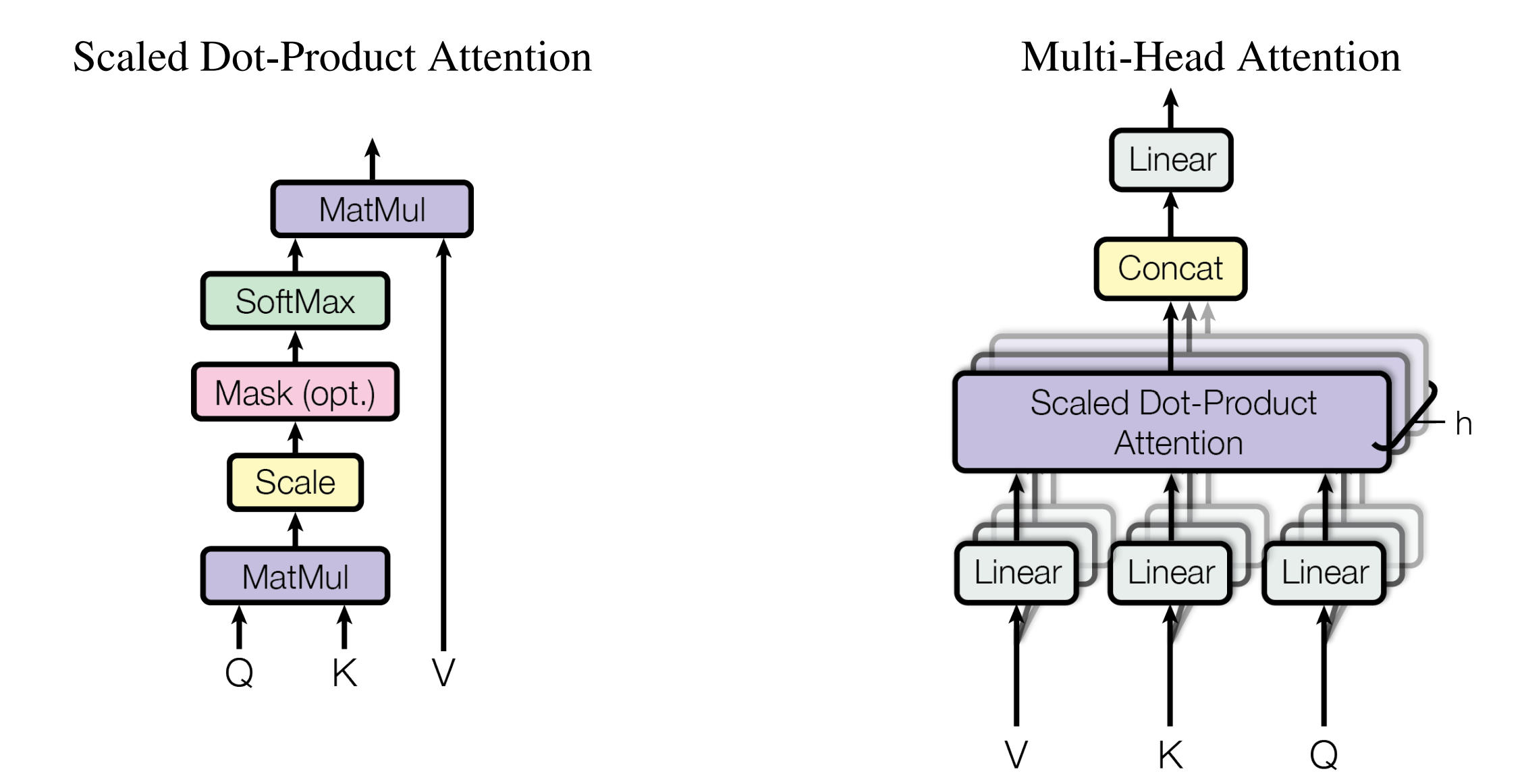
1.2、Scaled Dot-Product Attention

在这个模型中，query 和 key 的长度是等长的，都等于 $d_k$。value 的维度是 $d_v$，输出的维度也是 $d_v$。注意力的具体计算是：对每一个 query 和 key 做内积，然后把它作为相似度。

两个向量做内积：如果这两个向量的 norm 是一样的话，那么内积的值越大，它的余弦值越大，这两个向量的相似度就越高。如果你的内积的值为 0 ，这两个向量正交了，没有相似度。

例如，在一句句子中，一个名词的 query 可能代表：有没有修饰我的形容词？某个形容词的 key 可能代表：我在这！我们希望这两个向量相似度大（在高维空间中指向同一个方向），这样放在他们上面的注意力权重就会大，这个名词就会被修饰。换句话说，上下文被考虑到了。

value 可以看作，如果 query 和 key 相似度高，那么这个形容词是修饰名词的，那么名词的向量应该偏移多少来表示这个形容词的影响。例如“塔”这个字，如果出现了“埃菲尔铁塔”作为修饰，那么这个“塔”的名词对应的向量应该偏移以代表更高更大的东西，如果又出现了“埃菲尔铁塔玩具”，那么这个“塔”的名词对应的向量应该再次偏移以代表更小的东西。

\[Attention(Q,K,V) = Softmax(\frac{QK^T}{\sqrt{d_k}}) \times V\]

使用 softmax ：一个 query 会跟 n 个 key-value pair 做内积，会产生 n 个相似度值。传入 softmax 得到 n 个非负、求和为 1 的权重值。把 softmax 得到的权重值 与 value 矩阵 V 相乘 得到 attention 输出。$d_k$ 是向量的长度。

在 Transformer 的大模型应用中有温度 T 这个参数，体现在 softmax 的公式中：

\[Softmax(x_i)=\frac{e^{x_i/T}}{\sum_{j}e^{x_j/T}}\]

温度 T 越大，分布越平滑，越容易取到原先小概率的东西，在GPT的应用中，T 越大，越容易取到低概率的词，输出会更加多样化。

实际计算中，会把多个 query 写成 一个矩阵，并行化运算。

  • $Q维度:(n,d_k)$
  • $K维度: (m, d_k)$
  • $QK^T维度：(n, d_k) \times (m, d_k)^T = (n, m) $

为什么要除以$\sqrt{d_k}$？防止softmax函数的梯度消失。 $d_k$ 比较大时 （2 个向量的长度比较长的时候），点积的值会比较大，或者会比较小。当值比较大的时候，相对的差距会变大，导致最大值 softmax会更加靠近于1，剩下那些值就会更加靠近于0。值就会更加向两端靠拢，算梯度的时候，梯度比较小。在 trasformer 里面一般用的 $d_k$ 比较大 (本文 512) ，除以$\sqrt{d_k}$是不错的选择。

再回过头来看名字：

  • dot-product 指使用了点积。
  • Scaled 指除以了$\sqrt{d_k}$

具体举个例子：

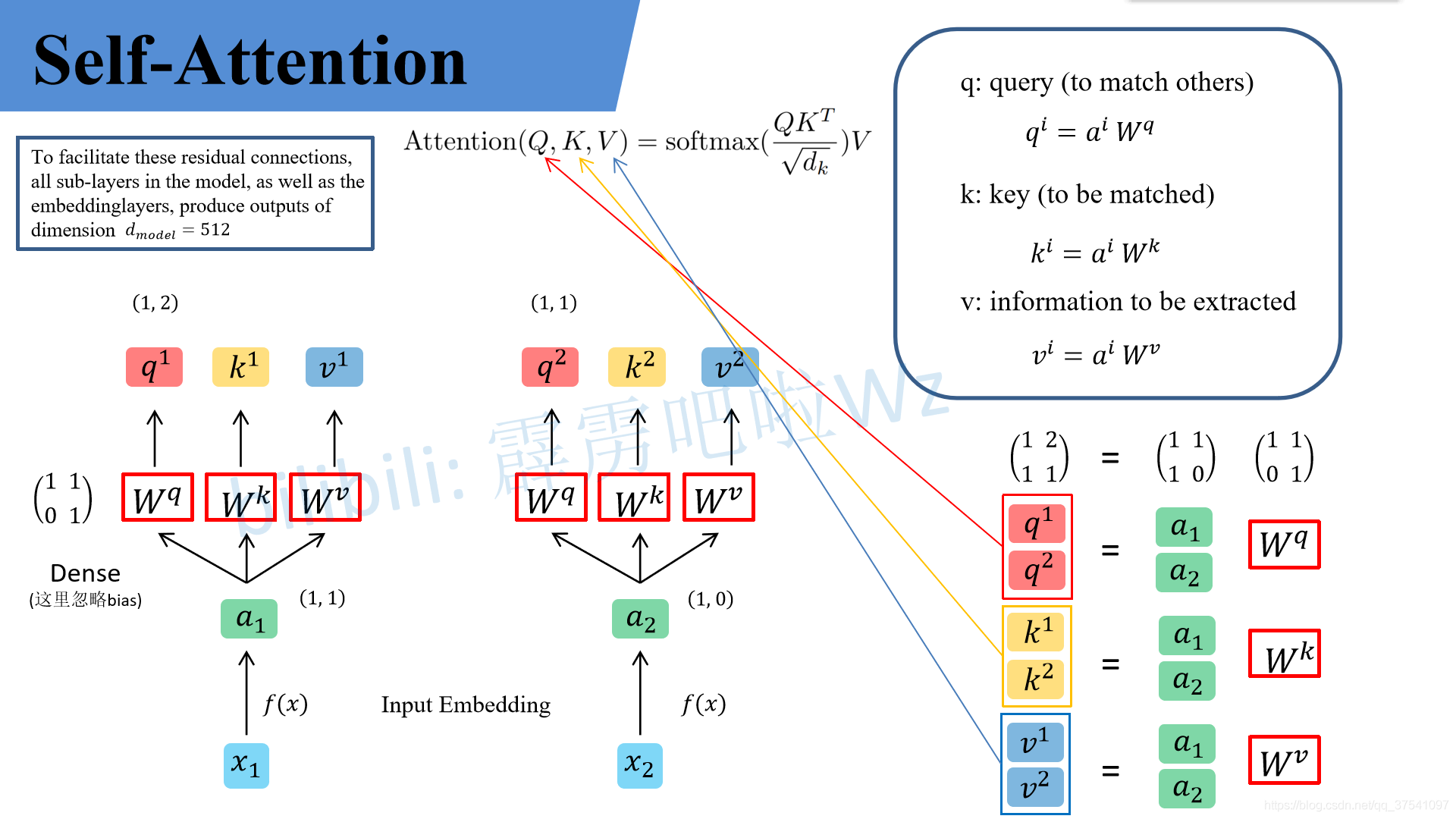
假设输入的序列长度为2，输入就两个节点$x_1, x_2$ ，然后通过Input Embedding也就是图中的f(x)，将输入映射到$a_1, a_2$，紧接着分别将 $a_1, a_2$ 分别通过三个变换矩阵 $W_q, W_k, W_v$ ，（这三个参数是可训练的，是共享的），得到 $q^i, k^i, v^i$，这里在源码中是直接使用全连接层实现的，这里为了方便理解，忽略偏置）。

其中

  • q 代表query，后续会去和每一个 k 进行匹配
  • k 代表key，后续会被每个 q 匹配
  • v 代表从 a 中提取得到的信息

后续 q 和 k 匹配的过程可以理解成计算两者的相关性，相关性越大对应 v 的权重也就越大。

假设 $a_1=(1, 1), a_2=(1,0), W^q= \binom{1, 1}{0, 1}$，那么：

\[q^1 = (1, 1) \binom{1, 1}{0, 1} =(1, 2) , \ \ \ q^2 = (1, 0) \binom{1, 1}{0, 1} =(1, 1)\]

前面有说Transformer是可以并行化的，所以可以直接写成：

\[Q= \binom{q^1}{q^2} = \binom{1, 1}{1, 0} \binom{1, 1}{0, 1} = \binom{1, 2}{1, 1}\]

同理得到 K 和 V，接着先拿 $q^1$ 每个 k 进行match，点乘操作，接着除以$\sqrt{d}$ 得到对应的 $\alpha$，其中 d 代表向量 $k^i$ 的长度，在本示例中等于2，比如计算 $\alpha_{1, i}$ ：

\[\alpha_{1, 1} = \frac{q^1 \cdot k^1}{\sqrt{d}}=\frac{1\times 1+2\times 0}{\sqrt{2}}=0.71 \\ \alpha_{1, 2} = \frac{q^1 \cdot k^2}{\sqrt{d}}=\frac{1\times 0+2\times 1}{\sqrt{2}}=1.41\]

同理拿$q^2$ 每个 k 进行match，统一写成矩阵乘法形式：

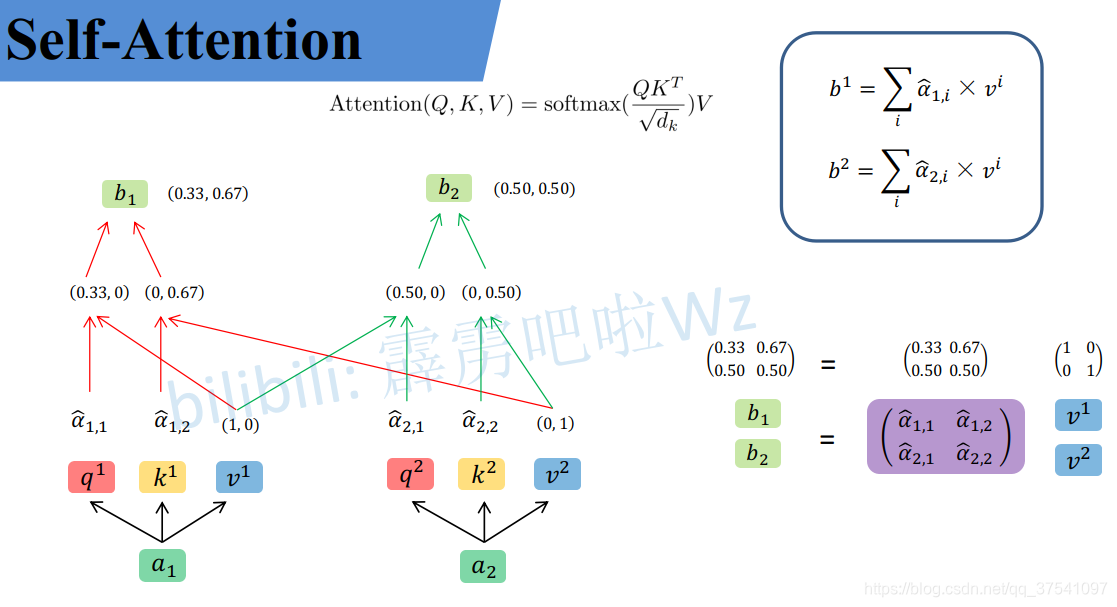
\[\binom{\alpha_{1, 1} \ \ \alpha_{1, 2}}{\alpha_{2, 1} \ \ \alpha_{2, 2}}=\frac{\binom{q^1}{q^2}\binom{k^1}{k^2}^T}{\sqrt{d}}\]

接着对每一行分别进行softmax处理得到 $(\hat\alpha_{1, 1}, \hat\alpha_{1, 2}), (\hat\alpha_{2, 1}, \hat\alpha_{2, 2})$，相当于计算得到针对每个 v 的权重。到这我们就完成了 Attention(Q,K,V)公式中 ${\rm softmax}(\frac{QK^T}{\sqrt{d_k}})$部分。

接着进行加权得到最终结果：

\[b_1 = \hat{\alpha}_{1, 1} \times v^1 + \hat{\alpha}_{1, 2} \times v^2=(0.33, 0.67) \\ b_2 = \hat{\alpha}_{2, 1} \times v^1 + \hat{\alpha}_{2, 2} \times v^2=(0.50, 0.50)\]

统一写成矩阵乘法形式：

\[\binom{b_1}{b_2} = \binom{\hat\alpha_{1, 1} \ \ \hat\alpha_{1, 2}}{\hat\alpha_{2, 1} \ \ \hat\alpha_{2, 2}}\binom{v^1}{v^2}\]

总结下来就是论文中的一个公式：

\[{\rm Attention}(Q, K, V)={\rm softmax}(\frac{QK^T}{\sqrt{d_k}})V\]

自注意力和交叉注意力：

  • 自注意力的 Q和K 都来自同一个句子
  • 交叉注意力的 Q 和 K 来自不同的地方，例如一个英语句子和一个法语句子，这种情况下交叉注意力可以代表英语句子中的一个词对应法语句子中的一个词。

1.3、Masked Attention

Masked 意思是遮盖，指避免在 t 时刻看到 t 时刻以后的输入。 Mask只在Decoder端进行,目的是为了使得decoder不能看见未来的信息。具体指在计算权重的时候，t 时刻只用了 $v_1, …, v_{t-1}$ 的结果，不要用到 t 时刻以后的内容。

如果我们把注意力看作上下文信息的交流，由于在输出时看不到未来的信息，这些注意力权重应当为0

Mask 非常简单，首先生成一个下三角全 0，上三角全为负无穷的矩阵（ t 时刻以后 $Q_t$ 和 $K_t$ 的值换成一个很大的负数），然后将其与 Scaled Scores 相加即可：

之后再做 softmax，就能将 - inf 变为 0，得到的这个矩阵即为每个字之间的权重。

1.4、Multi-head attention

与其做一个单个的注意力函数，不如说把整个 query、key、value 整个投影到 1个低维，投影 h 次。然后再做 h 次的注意力函数，把每一个函数的输出 拼接在一起，然后再次投影，得到最终的输出。

为什么要做多头注意力机制呢？一个点乘的注意力里面，没有什么可以学的参数。为了识别不一样的模式，希望有不一样的计算相似度的办法。 先投影到低维，投影的 W 是可以学习的。 multi-head attention 给 h 次机会去学习 不一样的投影的方法，使得在投影进去的度量空间里面能够去匹配不同模式需要的一些相似函数，然后把 h 个 heads 拼接起来，最后再做一次投影。

\[head_i=Attention(QW_i^Q,KW_i^K,VW_i^V)\] \[MutiHead(Q,K,V) = Concat(head_1 ,...,head_h)W^O\]

本文采用 8 个 heads。因为有残差连接的存在使得输入和输出的维度至少是一样的。投影维度 $d_v = d_{model} / h = 512 / 8 = 64$，每个 head 得到 64 维度，拼接，再投影回 $d_{model}$。

使用 Pytorch 实现的自注意力层参考代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

class MultiHeadAttention(nn.Module):
    def __init__(self, heads, d_model, dropout = 0.1):
        super().__init__()
        self.d_model = d_model
        self.d_k = d_model // heads  # 分配到每个头的维度
        self.h = heads
        self.q_linear = nn.Linear(d_model, d_model)
        self.v_linear = nn.Linear(d_model, d_model)
        self.k_linear = nn.Linear(d_model, d_model)
        self.dropout = nn.Dropout(dropout)
        self.out = nn.Linear(d_model, d_model)
        
    def attention(q, k, v, d_k, mask=None, dropout=None):
        """
        q,k,v 的 shape 都是 (batch_size, heads, seq_len, d_k)
        """

        # transpose是 PyTorch 中的一个函数，用于交换张量的两个维度。
        # 这里交换 k 的最后两个维度，作用就等同于矩阵的转置操作。
        scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(d_k)

        # 掩盖掉那些为了填补长度增加的单元，使其通过 softmax 计算后为 0
        if mask is not None:
            mask = mask.unsqueeze(1)
            scores = scores.masked_fill(mask == 0, -1e9)

        scores = F.softmax(scores, dim=-1)  # 在最后一个维度上进行 softmax
        if dropout is not None:
            scores = dropout(scores)
        output = torch.matmul(scores, v)
        return output

    def forward(self, q, k, v, mask=None):
        bs = q.size(0)  # batch_size
        # 进行线性操作划分为成 h 个头
        k = self.k_linear(k).view(bs, -1, self.h, self.d_k)  # bs, seq_len, heads, d_k
        q = self.q_linear(q).view(bs, -1, self.h, self.d_k)
        v = self.v_linear(v).view(bs, -1, self.h, self.d_k)
        # 矩阵转置
        k = k.transpose(1,2)  # bs, heads, seq_len, d_k
        q = q.transpose(1,2)
        v = v.transpose(1,2)
        # 计算 attention
        scores = attention(q, k, v, self.d_k, mask, self.dropout)

        # 连接多个头并输入到最后的线性层
        # contiguous() 函数用于返回一个内存连续的有相同数据的 tensor，
        # 当我们对张量进行某些操作虽然张量的形状可能会改变，但是在内存中的数据并不会重新排列
        # 但是有些操作（如 view）要求张量在内存中是连续的，否则会抛出错误。
        concat = scores.transpose(1,2).contiguous().view(bs, -1, self.d_model)  # bs, seq_len, d_model
        output = self.out(concat)
        return output

1.5、Applications of attentions in our model

encoder 的注意力层

句子长度是 n，encoder 的输入是一个 n 个长为 d 的向量。它复制成了三下：同样一个东西，既 key 也作为 value 也作为 query，所以叫做自注意力机制。key、value 和 query 其实就是一个东西，就是自己本身。

输入了 n 个 query，每个 query 会得到一个输出，那么会有 n 个输出。输出 是 value 加权和（权重是 query 和 key 的相似度），输出的维度同样是 d

decoder 的 masked multi-head attention

同样输入复制三份，masked 体现在，看不到 t 时刻以后的输入。

decoder 的 multi-head attention

key-value 来自 encoder 的输出。 query 是来自 decoder 里 masked multi-head attention 的输出。

举个例子 在翻译Hello World 到 你好世界 的过程中，计算 “好” 的时候，“好”作为 query ，会跟 “hello” 向量更相近一点，给 “hello” 向量一个比较大的权重。但是 “world” 跟后面的词相关， “world” 跟 当前的query （“好” ）相关度没那么高。

在算 query “世” 的时候，会给第二个 “world” 向量，一个比较大的权重。

根据解码器的输入的不一样，会根据当前的 query 向量，去在编码器的输出里面去挑query感兴趣的东西。

2、LayerNorm

2.1、二维情况

每一行是一个样本 X，每一列是一个 feature。

BatchNorm：每次把一列（1 个 feature）放在一个 mini-batch 里，均值变成 0， 方差变成 1 的标准化。 公式为$(该列向量 - mini_batch 该列向量的均值)/(mini_batch 该列向量的方差)$。训练时使用mini-batch 计算均值，测试时：使用 全局 均值、方差。

LayerNorm：对每个样本做 Normalization（把每一行变成 均值为 0、方差为 1），不是对每个特征做 normalization。LayerNorm 整个把数据转置一次，放到 BatchNorm 里面出来的结果，再转置回去，基本上可以得到LayerNorm的结果。

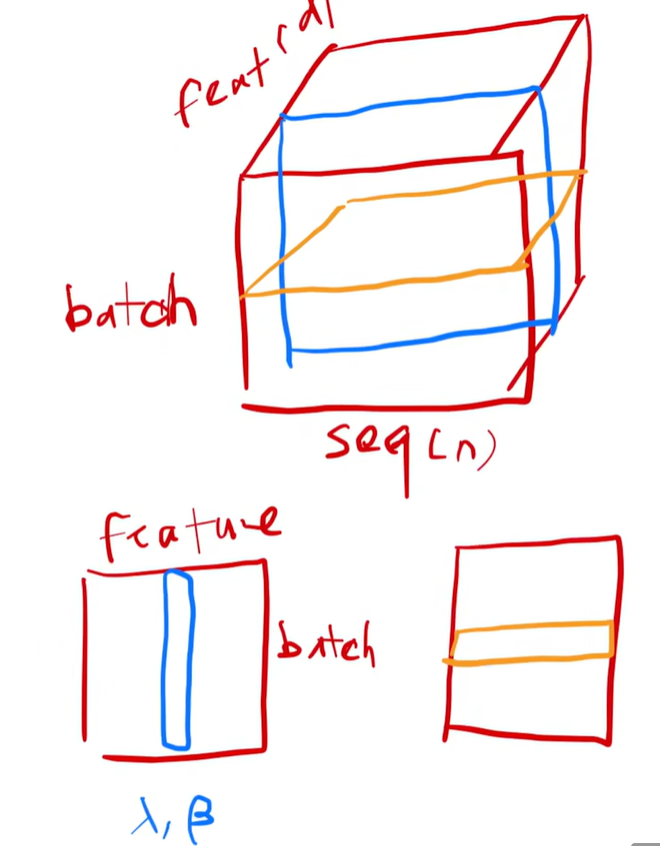
2.2、三维情况

输入的是一个序列的样本，每个样本中有很多元素，是一个序列。一个句子里面有 n 个词，每个词对应一个向量，加上batch维度，一共三维。

BatchNorm 每次取一个特征，切一块（蓝色线），拉成一个向量，均值为 0 、方差为 1 的标准化。

LayerNorm (橙色)，横着切。

2.3、为什么是LayerNorm？

时序数据中 样本长度可能不一样。BatchNorm需要补0，LayerNorm不需要， LayerNorm 更稳定，不管样本长还是短，均值和方差是在每个样本内计算。

层归一化的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

class NormLayer(nn.Module):
    def __init__(self, d_model, eps = 1e-6):
        super().__init__()
        self.size = d_model
        # 层归一化包含两个可以学习的参数，Parameter可以被注册为模型的一部分
        self.alpha = nn.Parameter(torch.ones(self.size))
        self.bias = nn.Parameter(torch.zeros(self.size))
        self.eps = eps
        
    def forward(self, x):
        # dim = -1 代表最后一个维度，keepdim = True 保持输出维度和输入维度一致
        norm = self.alpha * (x - x.mean(dim=-1, keepdim=True)) 
        / (x.std(dim=-1, keepdim=True) + self.eps) + self.bias
        return norm

3、Position-wise Feed-Forward Networks

说白了是作用在最后一个维度的 MLP 。

Point-wise: 把一个 MLP 对每一个词 （position）作用一次。

单隐藏层的 MLP，中间 W1 扩维到4倍 2048，最后 W2 投影回到 512 维度大小，便于残差连接。 \(FFN(x) = max(0, xW_1 + b_1)W_2 + b_2\) pytorch实现：2个线性层。pytorch在输入是3d的时候，默认在最后一个维度做计算。

参考代码如下：

1
2
3
4
5
6
7
8
9
10
11

class FeedForward(nn.Module):
    def __init__(self, d_model, d_ff=2048, dropout = 0.1):
        super().__init__()
        # d_ff 默认设置为 2048
        self.linear_1 = nn.Linear(d_model, d_ff)
        self.dropout = nn.Dropout(dropout)
        self.linear_2 = nn.Linear(d_ff, d_model)
        
    def forward(self, x):
        x = self.dropout(F.relu(self.linear_1(x)))
        x = self.linear_2(x)

4、Positional Encoding

在做attention的时候，output 是 value 的 加权和（权重是 query 和 key 之间的距离，和 序列信息 无关）。attention 不会有时序信息。 因此，根本不看 key - value 对在序列哪些地方。一句话把顺序任意打乱之后，attention 出来，结果都是一样的。顺序会变，但是值不会变，有问题！

需要加入时序信息。 如果使用RNN，把上一时刻的输出 作为下一个时刻的输入，来传递时序信息。 attention 在输入里面加入时序信息，叫做 positional encoding。公式为：

\[PE_{(pos,2i)} = sin(\frac{pos}{n^{2i/d_{model}}})\] \[PE_{(pos,2i+1)} = cos(\frac{pos}{n^{2i/d_{model}}})\]
  • \(d_{model}\)：输出嵌入空间的维度，如果一个词在嵌入层是一个长度为512的向量，那么使用一个长为512的向量来表示一个位置的数字。
  • \(n\)：用户定义的标量，由 Attention Is All You Need 的作者设置为 10,000。

在上面的表达式中，可以看到偶数位置对应于正弦函数，奇数位置对应于余弦函数。为了理解上面的表达式，我们以短语“I am a robots”为例，其中 n=100，d=4。下表显示了该短语的位置编码矩阵。事实上，对于任何 n=100 且 d=4 的四字母短语，位置编码矩阵都是相同的。

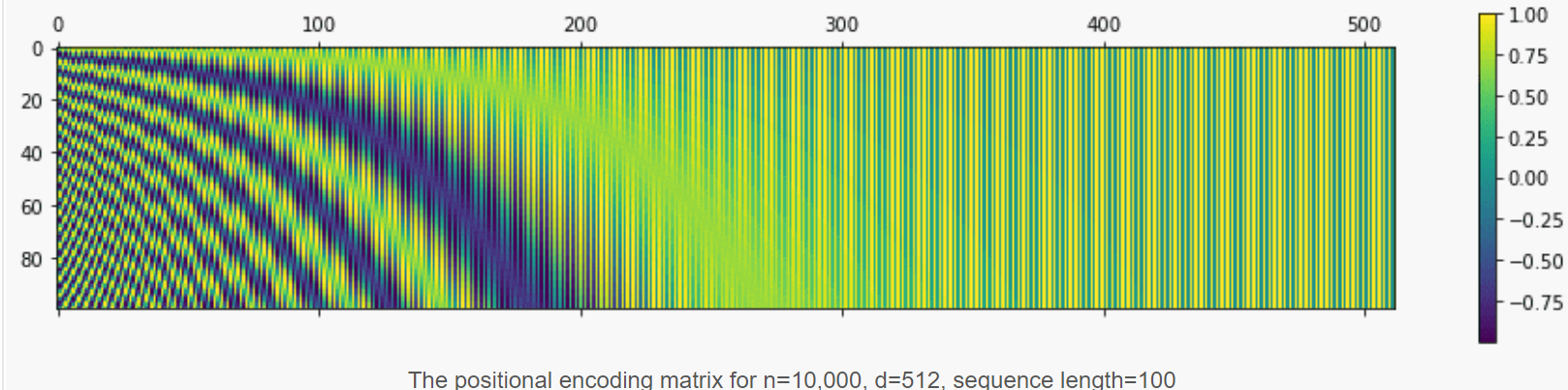
让我们将位置矩阵可视化为更大的值。按照原始论文中的方法设置 n=10000，d=512，length=100，将得到以下结果：

为了理解位置编码，我们首先查看 n=10,000 和 d=512 的不同位置的正弦波。横轴可以看作公式中的 i ，纵轴为输出的位置编码的值：

  • 正弦波的波长形成几何级数，并从 \(2\pi\) 到 \(2\pi n\) 变化
  • 正弦和余弦函数的值在 [-1, 1] 范围内，这将位置编码矩阵的值保持在标准化范围内
  • 这样编码可以表示相对位置，即关注一个token与另一个token距离差几个token。比如：位置1和位置2的距离比位置3和位置10的距离更近，位置1和位置2与位置3和位置4都只相差1。

可以证明：

\[PE_{pos} \cdot PE_{pos+k} = \sum_{i=0}^{\frac{d}{2}-1}cos(\frac{k}{n^{2\times i /d}})\]

相乘后的结果为一个余弦的加和。这里影响值的因素就是k。如果两个token的距离越大，也就是k越大，根据余弦函数的性质可以知道，两个位置向量的相乘结果越小。这样的关系可以得到，如果两个token距离越远则乘积的结果越小。

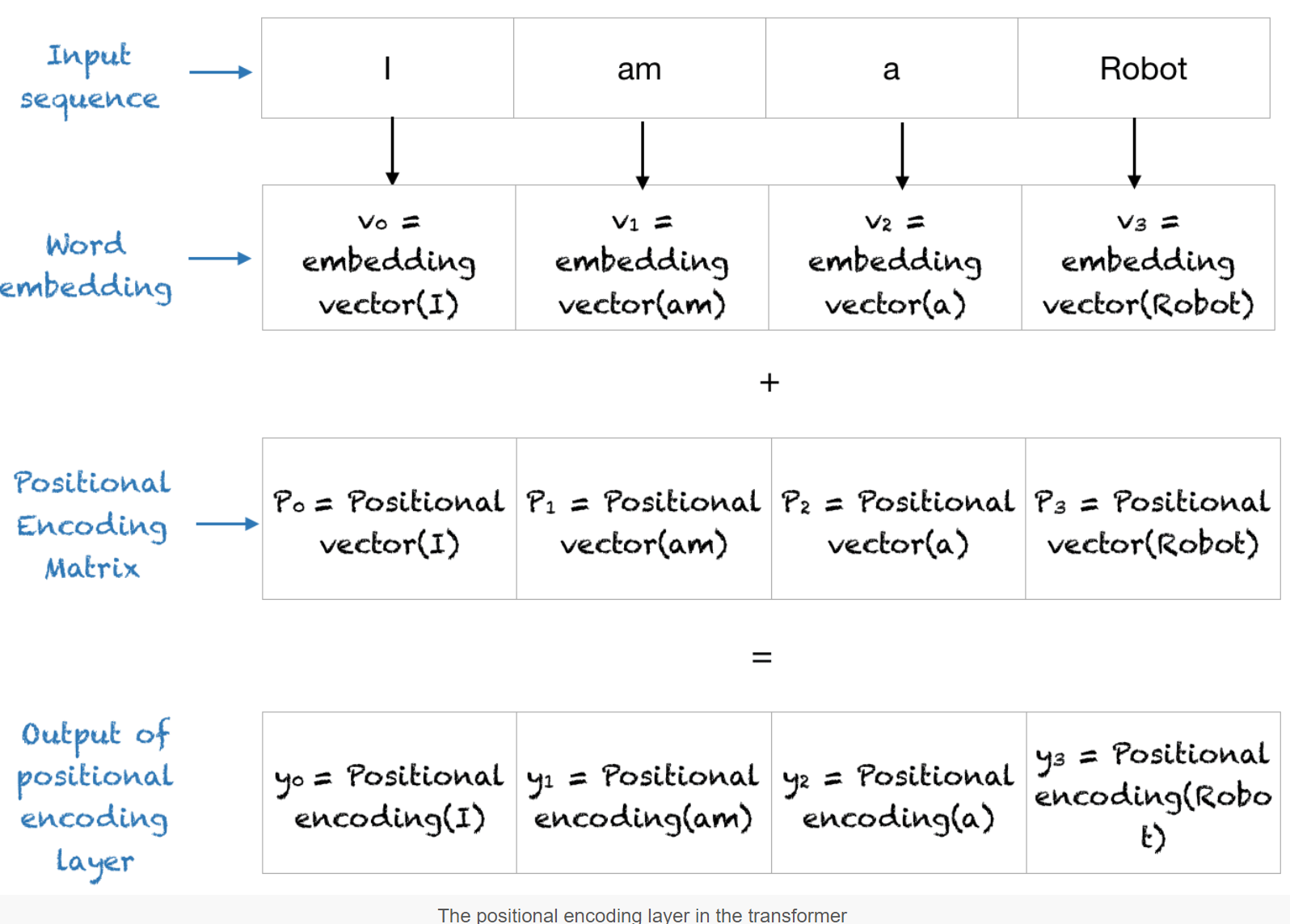
将这个东西与词向量相加，就得到了含有时序信息的向量。

看一下嵌入表示层的代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class PositionalEncoder(nn.Module):
    def __init__(self, d_model, max_seq_len = 80):
        super().__init__()
        self.d_model = d_model
        
        # 根据 pos 和 i 创建一个常量 PE 矩阵
        pe = torch.zeros(max_seq_len, d_model)
        for pos in range(max_seq_len):
            for i in range(0, d_model, 2):
                pe[pos, i] = math.sin(pos / (10000 ** ((2 * i)/d_model)))
                pe[pos, i + 1] = math.cos(pos / (10000 ** ((2 * (i + 1))/d_model)))
                
        pe = pe.unsqueeze(0)  # 增加维度，变成 1 * max_seq_len * d_model
        self.register_buffer('pe', pe)  # 注册为不可训练的参数

    def forward(self, x):
        x = x * math.sqrt(self.d_model)   # 使得单词嵌入表示相对大一些
        seq_len = x.size(1)  # 增加位置常量到单词嵌入表示中

        # 从 self.pe 中取出的一个切片，取所有行和前 seq_len 列的元素。
        # Variable将上述切片包装成一个 PyTorch 变量。
        # requires_grad=False 表示在反向传播时，不需要计算这个变量的梯度。
        # 这将变量移动到 GPU 上
        # 将上述变量添加到 x 上
        x = x + Variable(self.pe[:,:seq_len], requires_grad=False).cuda()
        return x

5、训练和测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97

# 模型参数定义
d_model = 512
heads = 8
N = 6
src_vocab = len(EN_TEXT.vocab)
trg_vocab = len(FR_TEXT.vocab)
model = Transformer(src_vocab, trg_vocab, d_model, N, heads)

# 初始化模型参数
for p in model.parameters():
    if p.dim() > 1:  # 如果参数的维度大于1
        nn.init.xavier_uniform_(p)  # 使用均匀分布初始化参数

optim = torch.optim.Adam(model.parameters(), lr=0.0001, betas=(0.9, 0.98), eps=1e-9)

# 模型训练
def train_model(epochs, print_every=100):
    model.train()  # 设置模型为训练模式
    start = time.time()
    temp = start
    total_loss = 0
    for epoch in range(epochs):
        for i, batch in enumerate(train_iter):
            src = batch.English.transpose(0,1)
            trg = batch.French.transpose(0,1)
            # the French sentence we input has all words except
            # the last, as it is using each word to predict the next
            trg_input = trg[:, :-1]  # <eos> 标记不需要输入到模型中
            # the words we are trying to predict
            targets = trg[:, 1:].contiguous().view(-1)  # <sos> 标记不需要预测

            # create function to make masks using mask code above
            src_mask, trg_mask = create_masks(src, trg_input)  # 生成掩码
            preds = model(src, trg_input, src_mask, trg_mask)  # 前向传播
            optim.zero_grad()
            loss = F.cross_entropy(preds.view(-1, preds.size(-1)),
            results, ignore_index=target_pad)  # 计算损失
            loss.backward()  # 反向传播计算参数的梯度
            optim.step()  # 更新模型参数
            total_loss += loss.data[0]  # 累加损失

            # 输出训练信息
            if (i + 1) % print_every == 0:
                loss_avg = total_loss / print_every
                print("time = %dm, epoch %d, iter = %d, loss = %.3f, \
                %ds per %d iters" % ((time.time() - start) // 60,
                epoch + 1, i + 1, loss_avg, time.time() - temp,
                print_every))
                total_loss = 0
                temp = time.time()

# 模型测试
def translate(model, src, max_len = 80, custom_string=False):
    model.eval()  # 设置模型为评估模式

    if custom_sentence == True:  # 如果是自定义句子
        src = tokenize_en(src)  # 分词
        
        # 将句子中的每个单词转换为其在词汇表中的索引
        # 将索引列表包装在一个列表中，形成一个二维列表
        # 将二维列表转换为 LongTensor
        # 将 LongTensor 包装为 Variable
        # 将 Variable 放到 GPU 中
        sentence=Variable(torch.LongTensor([[EN_TEXT.vocab.stoi[tok] for tok in sentence]])).cuda()

        # 比较 src 和 input_pad，得到一个布尔张量，
        # 其中的每个元素表示 src 中对应位置的元素是否不等于 input_pad
        # 在布尔张量的倒数第二个维度增加一个维度
        src_mask = (src != input_pad).unsqueeze(-2)

        # 输入 src 和 src_mask，得到编码器的输出
        e_outputs = model.encoder(src, src_mask)

        outputs = torch.zeros(max_len).type_as(src.data)  # 创建输出列表，类型与 src 相同
        outputs[0] = torch.LongTensor([FR_TEXT.vocab.stoi['<sos>']])  # 将输出列表的第一个元素设置为 <sos> 标记

    # 每次循环，预测一个单词
    for i in range(1, max_len):
        # triu 返回矩阵的上三角部分，k=1 表示对角线上的元素也包含在内，其余元素为 0
        trg_mask = np.triu(np.ones((1, i, i), k=1).astype('uint8'))  
        trg_mask= Variable(torch.from_numpy(trg_mask) == 0).cuda()
        out = model.out(model.decoder(outputs[:i].unsqueeze(0), e_outputs, src_mask, trg_mask))
        out = F.softmax(out, dim=-1)

        # 从 out 中取出的一个切片，取所有行和最后一列的元素。
        # .data：这是获取 PyTorch 变量（Variable）中的数据。
        # .topk(k)：这是一个函数，用于从输入中找出最大的 k 个值及其对应的索引。
        # 在这里，k 等于 1，所以它会找出最大的一个值及其索引。
        # topk 函数返回两个值，第一个是最大的 k 个值，第二个是这些值对应的索引。
        val, ix = out[:, -1].data.topk(1)
        outputs[i] = ix[0][0]  # 将输出列表的第 i 个元素设置为预测的下一个单词的索引
        if ix[0][0] == FR_TEXT.vocab.stoi['<eos>']:
            break  # 如果预测的下一个单词是 <eos> 标记，就停止预测

    return ' '.join(
    [FR_TEXT.vocab.itos[ix] for ix in outputs[:i]]
    )  # 将输出列表中的索引转换为单词，并返回单词列表
深度学习
读论文
本文由作者按照 CC BY 4.0 进行授权
最近更新
文章内容

Multitask learning and benchmarking with clinical time series data

An Image Is Worth 16x16 Words： Transformers For Image Recognition At Scale