A Gentle Introduction to Graph Neural Networks
图神经网络GNN
参考:
图神经网络不同于只用于网格结构数据的传统模型:LSTM,CNN等。是一种处理广义拓扑图(将实体抽象成与大小形状无关的点,点之间连接成线形成的图)结构的数据,深入挖掘其特征和规律的工具。
历史
- 2005年,Marco Gori等人发表了论文,首次提出了GNN的概念,在此之前,处理图数据的方法是在数据的预处理阶段将图转换为用一组向量表示。这种处理方法会丢失很多的结构信息,得到的结果会严重依赖于对图的预处理,GNN的提出能够将学习过程直接架构在图数据之上。
- 2009年,进一步的阐述了图神经网络,提出了一种监督的方法来训练GNN,但是,早期的研究都是以迭代的方式,通过RNN传播邻居消息,直到达到稳定的固定状态来学习节点的表示。这种计算消耗极大。
- 2012年,CNN在CV上取得了很好的成绩,于是开始将卷积应用在GNN中。
- 2013年,Bruna等人提出了GCN,这时候的GCN是基于频域卷积的。后来又有很多人对它进行改进,拓展,但是频域卷积在计算时需要同时处理整个图,并且需要承担矩阵分解时很高的时间复杂度。
- 2016年,Kipf等人将频域卷积的定义简化,使图卷积操作能够在空域进行,极大提高了图卷积模型的计算效率,同时,由于卷积滤波的高效性,GCN模型在很多图数据相关任务上取得了很好的成绩。
- 之后的近几年里,更多的基于空域GCN的变体被开发出来。这类方法都统称为GNN。各种GNN模型,大大加强了对各类图数据的适应性。
- 2018年,该领域不约而同地同时发表3篇综述论文。
- 2019年,各大顶级学术会议上GNN占据很大份额。
定义
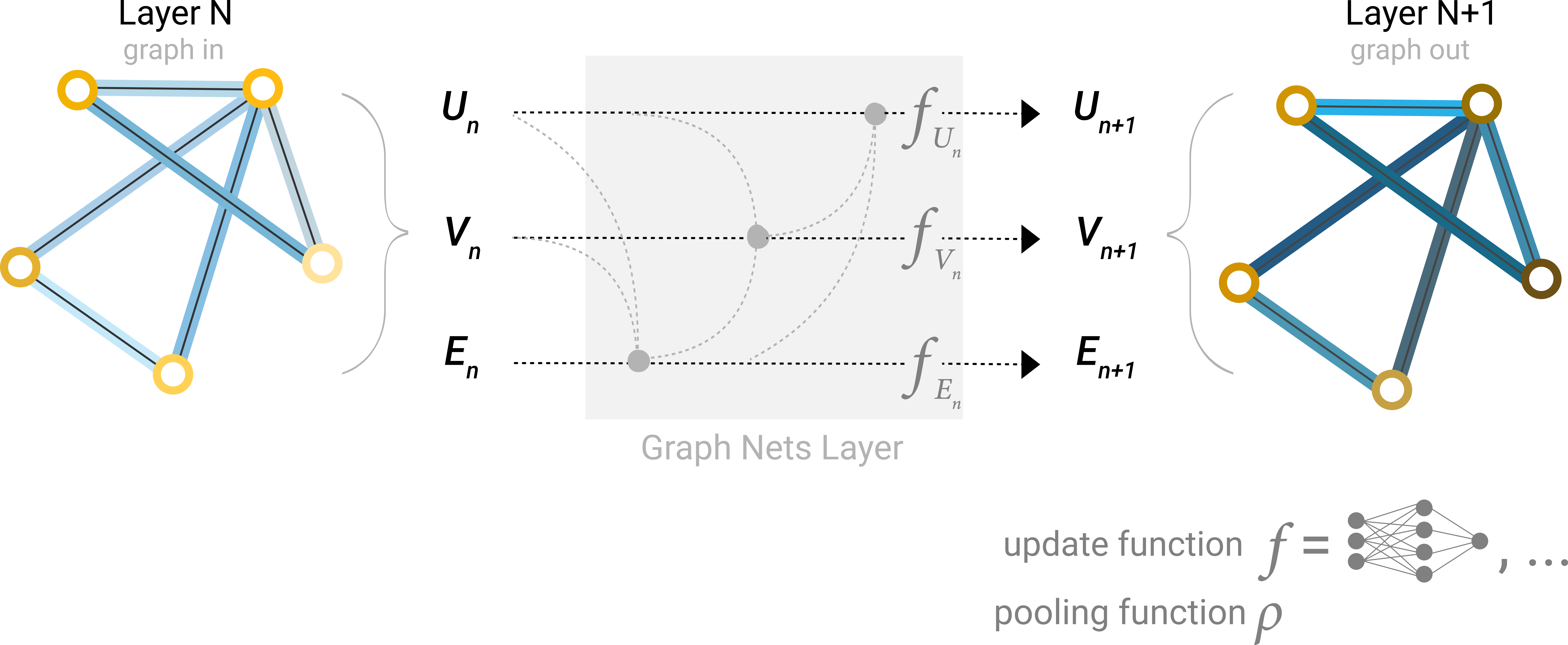
GNN 是对图的所有属性(节点、边、全局上下文)的可优化转换,它保留了图的对称性(排列不变性)。
我们可以将一个图的节点、边、全局都用一个向量来表示。
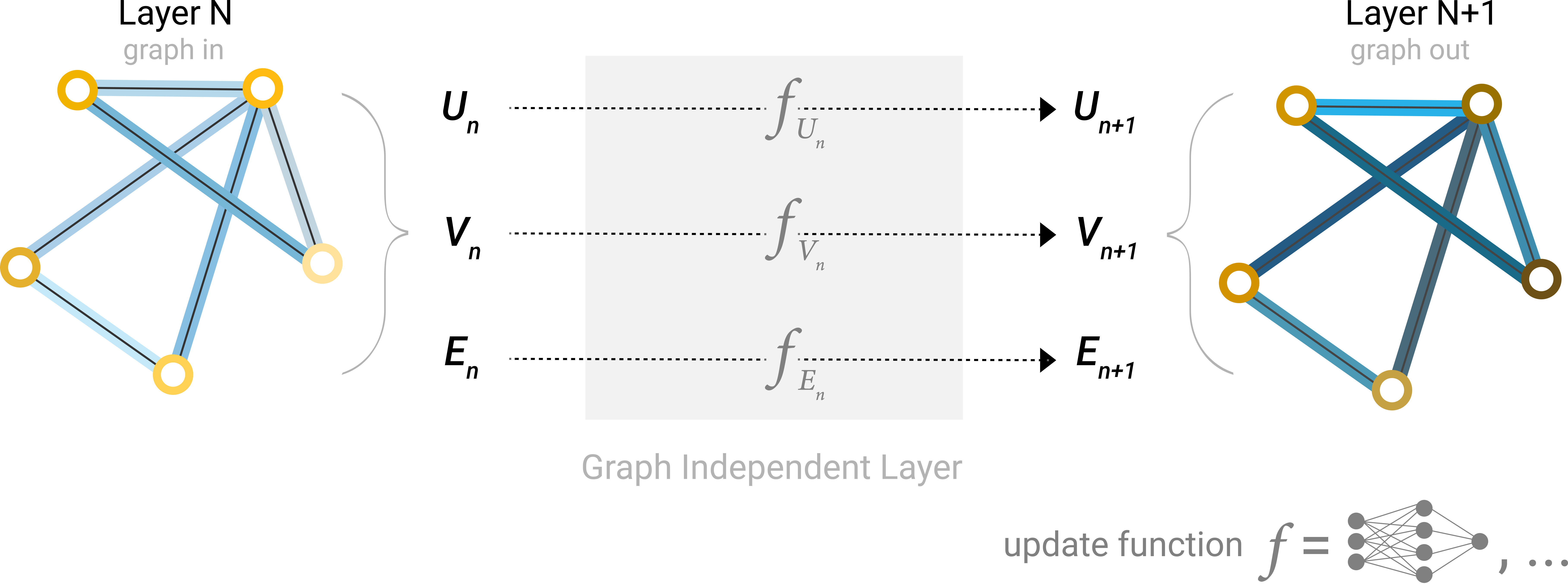
GNN 采用“图输入,图输出”架构,这意味着这些模型类型接受图作为输入,将信息加载到其节点、边缘和全局上下文中,并逐步转换这些嵌入,而不会改变输入图的连通性。
最简单的GNN
从最简单的 GNN 架构开始,在这个架构中,我们学习了所有图属性(节点、边、全局)的新嵌入,但我们还没有使用图的连通性。
这个GNN在图的每个组成部分上使用一个单独的多层感知器(MLP),我们称之为GNN层。对于每个节点向量、边向量、全局上下文向量,应用 MLP 并返回一个学习到的向量。
在这里,所有节点V使用同一个MLP,所有边E使用同一个MLP,全局上下文U就一个。
与神经网络模块或层一样,我们可以将这些GNN层堆叠在一起。
由于 GNN 不会更新输入图的连通性,因此我们可以描述具有与输入图相同的邻接列表和相同数量的特征向量的 GNN 的输出图。但是,输出图更新了嵌入,因为 GNN 更新了每个节点、边和全局上下文表示。
但是这个模型有明显的问题:
- 节点的信息和边的信息都是独立的,在学习的时候相互看不见。
- 整个图的结构信息没有使用上。
带池化的GNN
如果我们需要对节点进行预测,但是图形中的信息存储在边中,节点中没有信息,怎么办?
我们需要一种方法来从边收集信息并将其提供给节点进行预测。我们可以通过池化来做到这一点。池化分两步进行:
- 对于要池化的每个项目,收集它们的每个嵌入并将它们连接成一个矩阵。
- 然后,通常通过求和运算聚合收集的嵌入。
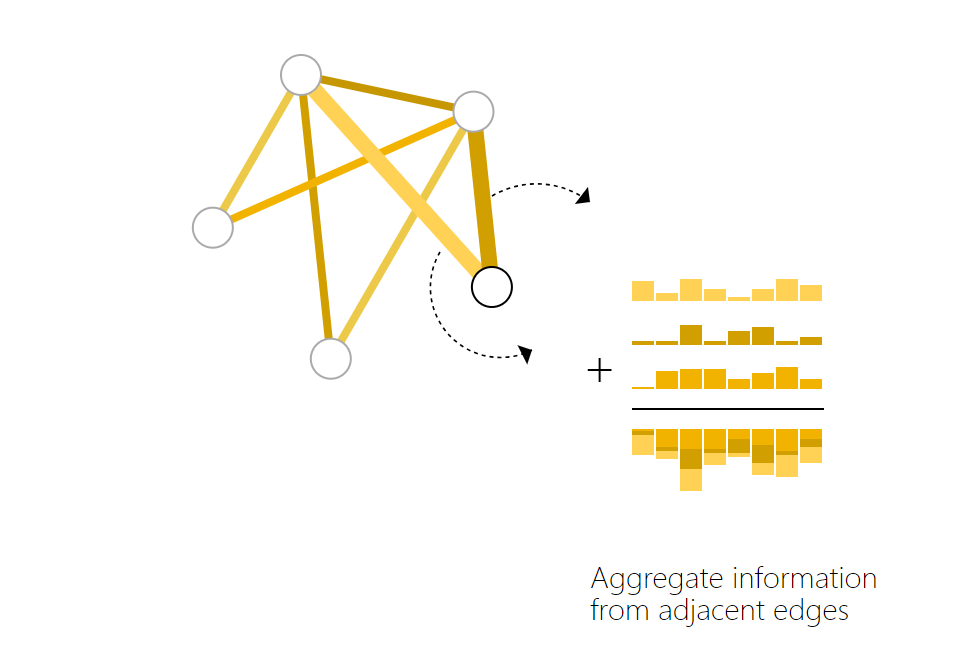
这个图中虽然只有两个箭头指向的两条边参与了这次池化操作,旁边加和的另外一个向量可能指的是全局信息。
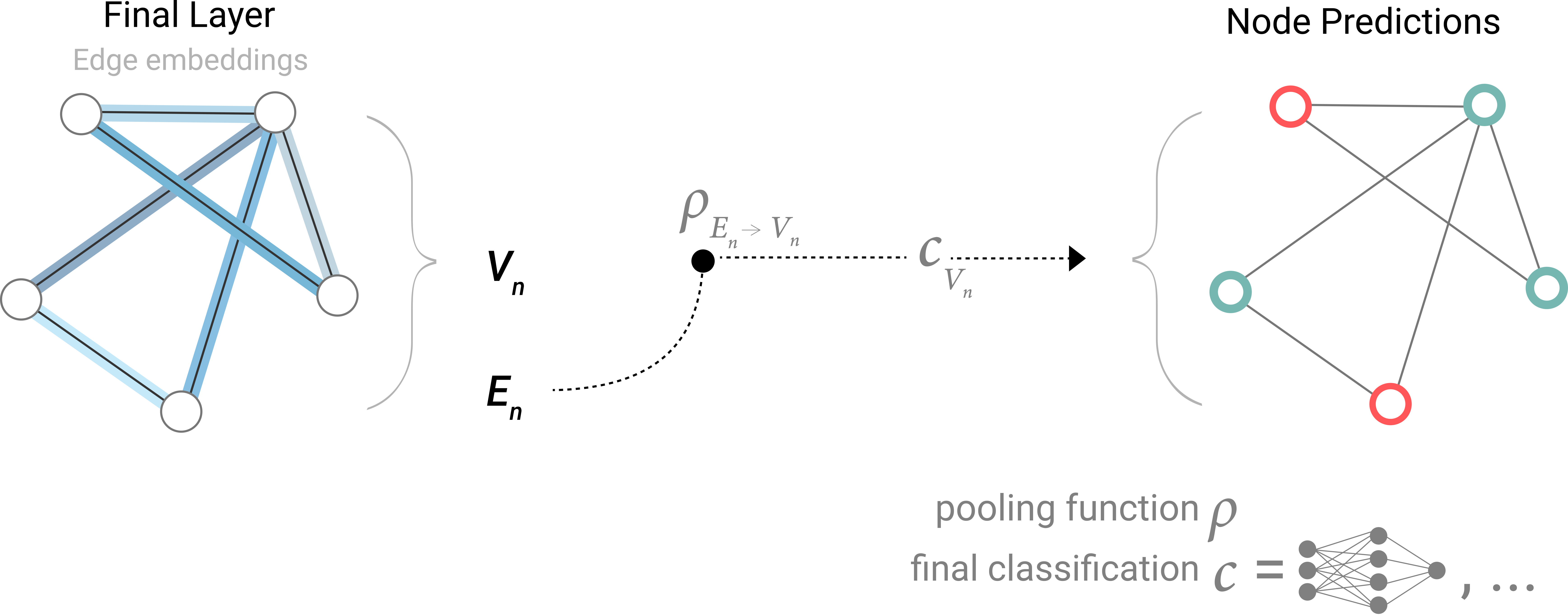
我们用字母 ρ 表示池化操作,并表示我们正在收集从边到节点的信息,如 $ρ_{E_n \to V_{n}}$
因此,如果我们只有边级特征,并试图预测节点信息,我们可以使用池化将信息路由(或传递)到需要去的地方。模型如下所示。
同样的,我们可以根据的节点信息预测全局属性或者边信息,诸如此类。
我们已经证明了我们可以构建一个简单的GNN模型,并通过在图形的不同部分之间路由信息来进行预测。这种池化技术将作为构建更复杂的GNN模型的构建块。如果我们有新的图形属性,我们只需要定义如何将信息从一个属性传递到另一个属性。
然而,整个图的结构信息没有使用上,例如图的一个点没有办法知道另外一侧的相隔很远的点的信息。
传递消息
点到点
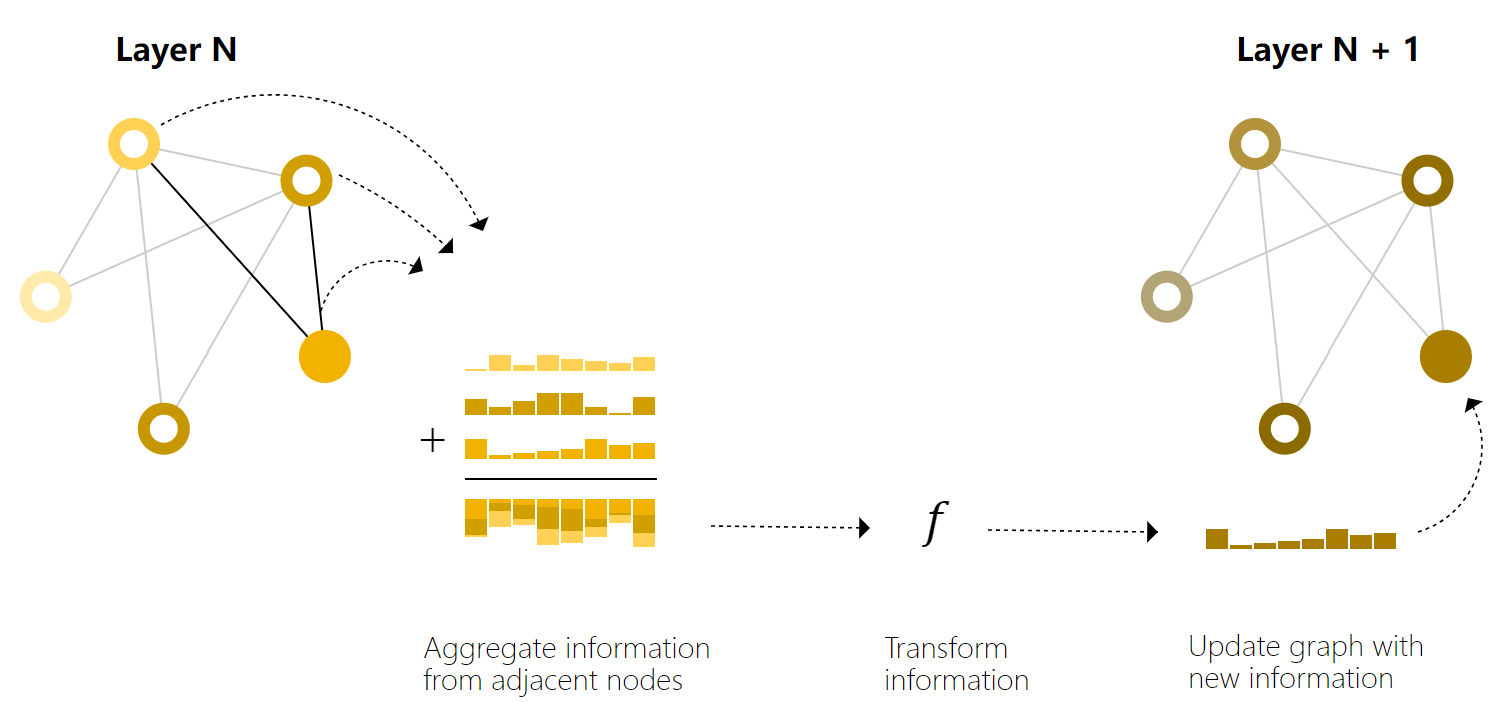
现在我们解决之前提到的问题,消息传递分三个步骤进行:
- 对于图中的每个节点,收集所有相邻的节点嵌入(或消息),这就是上面描述的 g 函数
- 通过聚合函数聚合所有消息(如 sum)
- 所有池化消息都通过更新函数(通常是学习的神经网络)传递
正如池化可以应用于节点或边缘一样,消息传递也可以发生在节点或边缘之间。
这些步骤是利用图形连接的关键。我们将在 GNN 层中构建更复杂的消息传递变体,以产生具有增强表现力和功率的 GNN 模型。
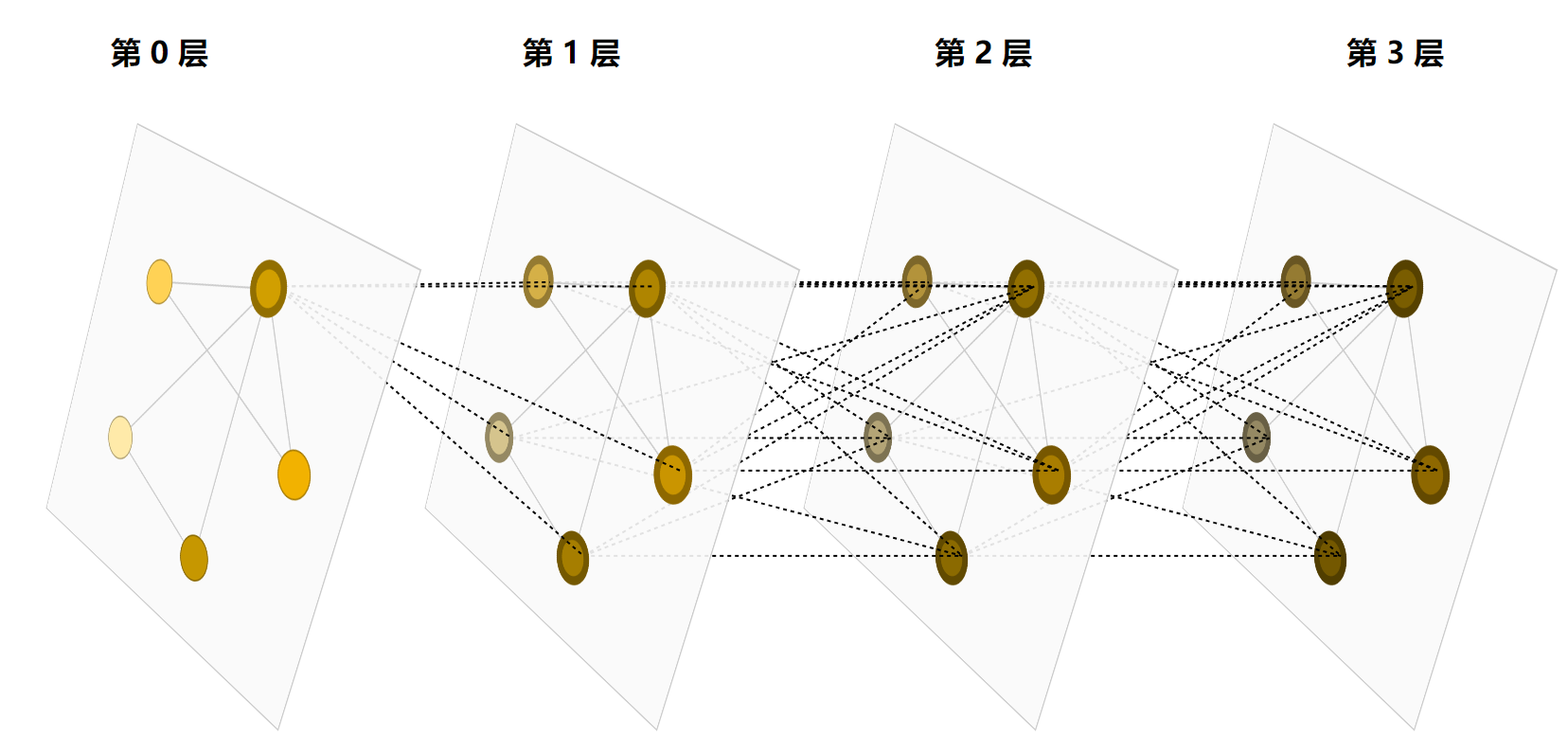
通过将传递GNN的消息层堆叠在一起,一个节点最终可以整合来自整个图的信息:在三层之后,一个节点拥有关于距离它三步远的节点的信息。
这让人想起标准卷积:从本质上讲,消息传递和卷积是聚合和处理元素邻居信息以更新元素值的操作。在图中,元素是一个节点,而在图像中,元素是一个像素。但是,图中相邻节点的数量可以是可变的,这与图像中每个像素都有一定数量的相邻元素不同。另外一点区别是图像中的卷积,因为存在核的概念,像素是权重不同的;但在图神经网络中的这个操作不存在权重,或者说所有相邻点的权重是相同的。
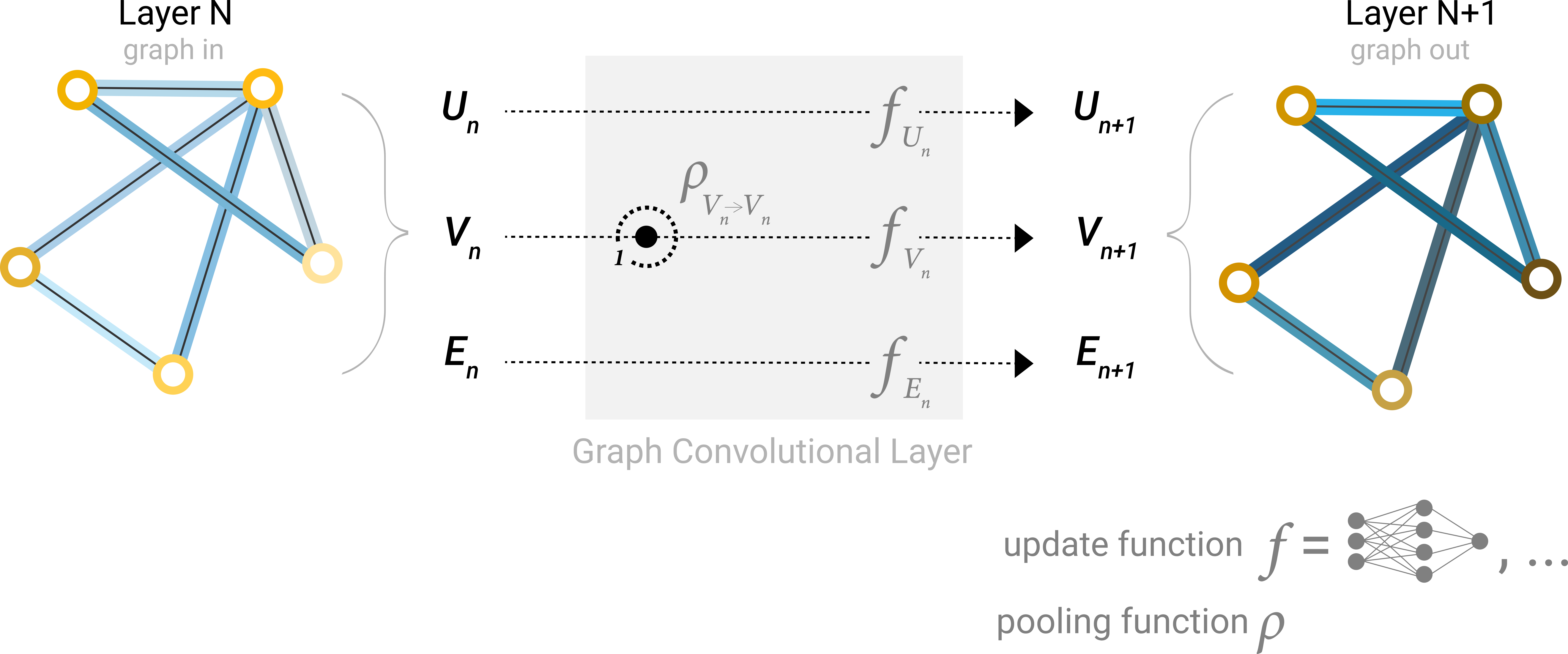
我们可以更新我们的架构图,以包含节点的这个新信息源:
存在一个问题:点只能与点共享信息,但是点获取不到边的信息,怎么办?
点与边
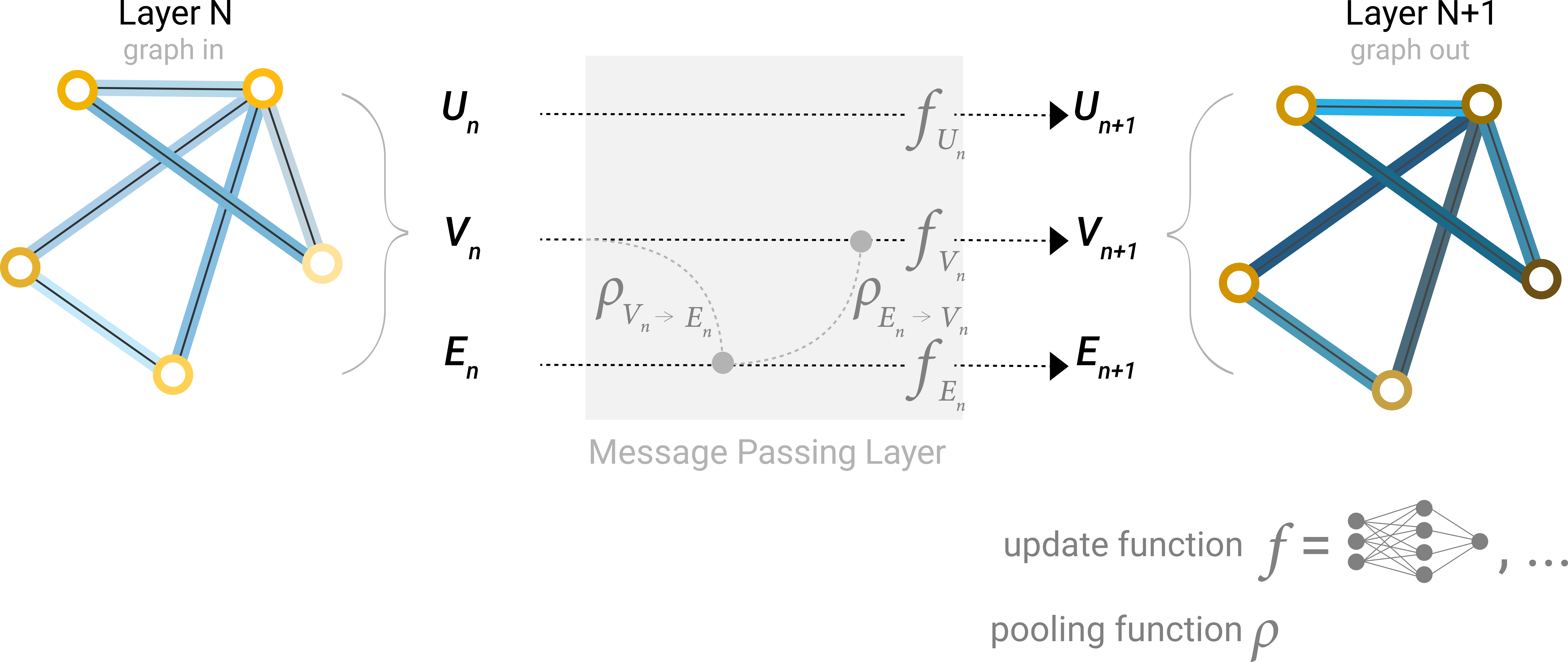
同样,我们可以使用消息传递在 GNN 层内的节点和边之间共享信息。
我们可以像之前使用相邻节点信息一样,通过首先汇集边缘信息,使用更新函数对其进行转换,然后存储它,来合并来自相邻边缘的信息。
不过,存储在图中的节点和边信息不一定具有相同的大小或形状,一种方法是学习从边空间到节点空间的线性映射,反之亦然。或者,可以在更新函数之前将它们连接在一起。
在构建 GNN 时,我们更新哪些图形属性以及更新它们的顺序是一个是一个具有各种解决方案的开放研究领域,例如:
- 在边嵌入之前更新节点嵌入,还是相反。
- 节点到节点
- 边到边
- 节点到边
- 边到节点
换句话说,边与节点之间的信息传递可以是很复杂的,可以远远比上图示意图更复杂更多联系。
全局消息
到目前为止,我们所描述的网络存在一个缺陷:即使我们多次应用消息传递,图中彼此相距较远的节点也可能永远无法有效地相互传输信息。例如,对于一个节点,如果我们有 k 层,信息最多会在 k 步之外传播。
此问题的一个解决方案是使用图的全局表示 U,有时称为主节点或上下文向量。这个全局上下文向量连接到网络中的所有其他节点和边缘,可以充当它们之间的桥梁来传递信息,从而为整个图形构建表示。这创建了比以其他方式学习的更丰富、更复杂的图形表示。
在这个视图中,所有图属性都学习了表示,因此我们可以在池化过程中通过调节我们感兴趣的属性相对于其余属性的信息来利用它们。例如,对于一个节点,我们可以考虑来自相邻节点、连接边和全局信息的信息。为了在所有这些可能的信息源上嵌入新节点,我们可以简单地将它们连接起来。此外,我们还可以通过线性映射将它们映射到同一空间,并添加它们或应用特征调制层,这可以被认为是一种特征性注意力机制。
实验
展示了一个带有小分子图的图形级预测任务。我们使用Leffingwell气味数据集,该数据集由具有相关气味感知(标签)的分子组成。预测分子结构(图形)与其气味的关系是一个有100年历史的问题,横跨化学、物理学、神经科学和机器学习。
为了简化问题,我们只考虑每个分子的单个二元标记,对分子图是否闻起来“刺鼻”进行分类,如专业调香师标记的那样。如果一个分子具有强烈、引人注目的气味,我们就会说它有一种“刺鼻”的气味。例如,可能含有烯丙醇分子的大蒜和芥末具有这种品质。通常用于薄荷味糖果的分子胡椒酮也被描述为具有刺鼻的气味。
我们将每个分子表示为一个图,其中原子是包含其原子同一性(碳、氮、氧、氟)的独热编码的节点,键是包含独热编码其键类型(单键、双键、三键或芳香族)的边缘。
我们将使用连续的 GNN 层构建针对此问题的通用建模模板,然后使用具有 S 形激活的线性模型进行分类。我们的 GNN 的设计空间有许多可以自定义模型的杠杆:
- GNN 层数,也称为深度。
- 更新时每个属性的维度。更新函数是一个 1 层 MLP,具有 relu 激活函数和用于激活归一化的层范数。
- 池化中使用的聚合函数:最大值、平均值或总和。
- 更新的图形属性或消息传递的样式:节点、边和全局表示。我们通过布尔切换(打开或关闭)来控制它们。基线模型将是一个与图形无关的 GNN(所有消息传递),它将末尾的所有数据聚合到一个全局属性中。切换所有消息传递函数会产生 GraphNets 架构。
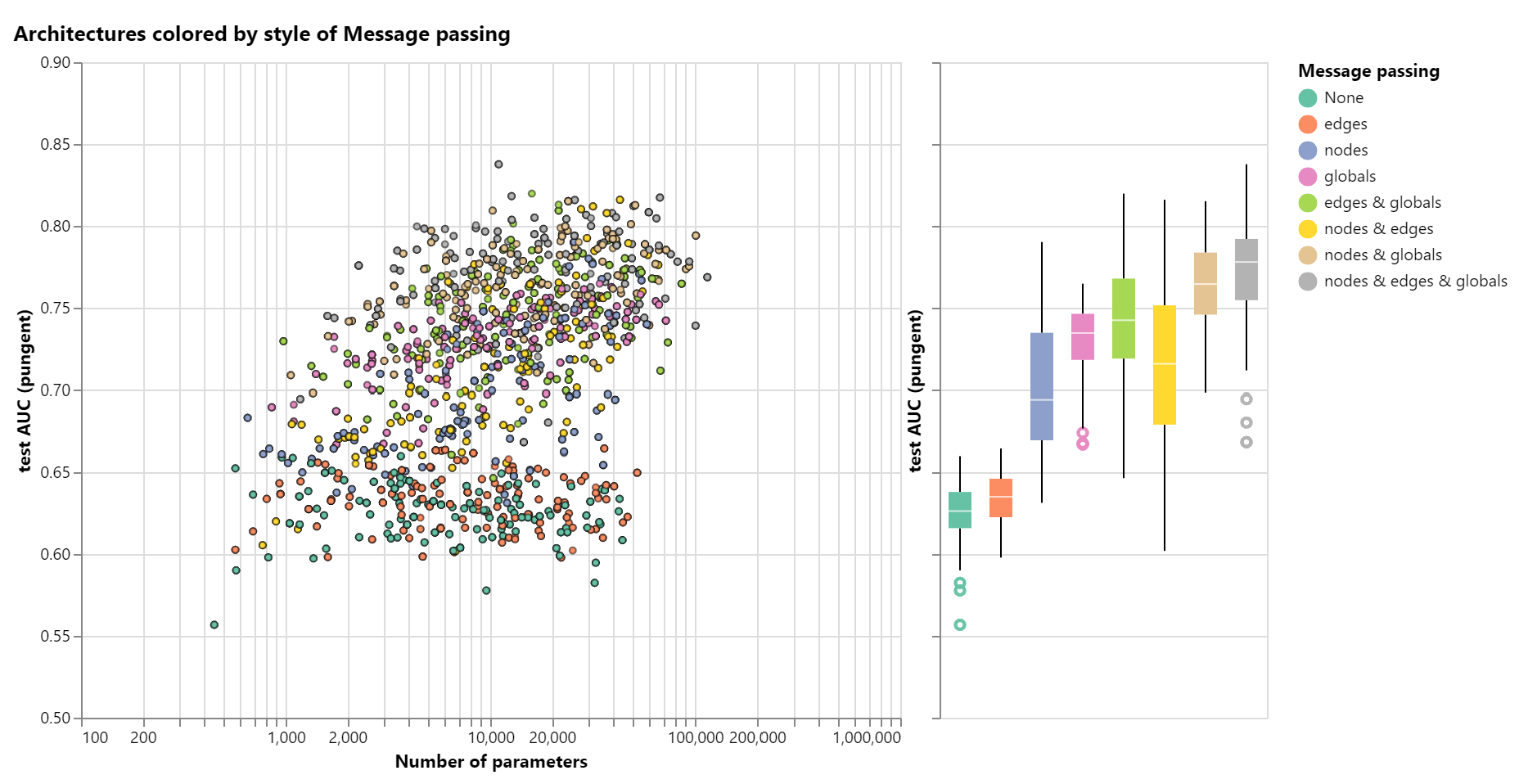
一些实验结果:
- 更多的参数确实与更高的性能相关。
- GNN是一种参数效率非常高的模型类型:即使是少量的参数(3k),我们也已经可以找到高性能的模型。
- 具有较高维数的模型往往具有更好的均值和下限性能。
- 三种池化中使用的聚合函数:最大值、平均值或总和,表现类似。
- 平均性能倾向于随着层数的增加而增加。但是如果不好好调参,层数多的模型效果也可能很差。这从另外一个角度上表明,图神经网络是一个对参数高度敏感的模型。
- 图属性的交流越多,平均模型的性能就越好。